Cap. 11 - Estimadores de riqueza
# Pacotes necessários
library(iNEXT)
library(ecodados)
library(ggplot2)
library(vegan)
library(nlme)
library(dplyr)11.1 Carregue os dados - Cap11_exercicio1 - que está no pacote ecodados. Este conjunto de dados representa a abundância de 50 espécies de besouros coletados em 30 amostras. Calcule os estimadores de riqueza - Chao1 e ACE - e faça um gráfico contendo a riqueza observada e os dois estimadores de riqueza. Qual a sua interpretação sobre o esforço amostral?
Solução:
# Carregar a planilha com os dados
exercicio_1 <- ecodados::Cap11_exercicio1
# estimadores abundância
est_abun <- estaccumR(exercicio_1, permutations = 100)
## Preparando os dados para fazer o gráfico
resultados_abun <- summary(est_abun
, display = c("S", "chao", "ace"))
res_abun <- cbind(resultados_abun$chao[, 1:4], resultados_abun$ace[, 2:4],
resultados_abun$S[, 2:4])
res_abun <- as.data.frame(res_abun)
colnames(res_abun) <- c("Amostras", "Chao", "C_inferior", "C_superior",
"ace", "A_inferior", "A_superior",
"Riqueza", "R_inferior", "R_superior")
## Gráfico
ggplot(res_abun, aes(y = Riqueza, x = Amostras)) +
geom_point(aes(y = Chao, x = Amostras + 0.1), size = 4,
color = "darkorange", alpha = 1) +
geom_point(aes(y = ace, x = Amostras + 0.2), size = 4,
color = "cyan4", alpha = 1) +
geom_point(aes(y = Riqueza, x = Amostras), size = 4,
color = "black", alpha = 1) +
geom_point(y = 150, x = 1, size = 4, color = "darkorange", alpha = 1) +
geom_point(y = 135, x = 1, size = 4, color = "cyan4", alpha = 1) +
geom_point(y = 120, x = 1, size = 4, color = "black", alpha = 1) +
geom_label(y = 150, x = 4.4, label = "Chao 1", size = 5) +
geom_label(y = 135, x = 3.9, label = "ACE", size = 5) +
geom_label(y = 120, x = 7.3, label = "Riqueza observada", size = 5) +
geom_line(aes(y = Chao, x = Amostras), color = "darkorange") +
geom_line(aes(y = ace, x = Amostras), color = "cyan4") +
geom_line(aes(y = Riqueza, x = Amostras), color = "black") +
geom_linerange(aes(ymin = C_inferior, ymax = C_superior,
x = Amostras + 0.1), color = "darkorange") +
geom_linerange(aes(ymin = A_inferior, ymax = A_superior,
x = Amostras + 0.2), color = "cyan4") +
geom_linerange(aes(ymin = R_inferior, ymax = R_superior,
x = Amostras), color = "black") +
scale_x_continuous(limits = c(1, 31), breaks = seq(1, 31, 1)) +
labs (x = "Número de amostras", y = "Riqueza de espécies de besouros") +
theme_bw(base_size = 12) +
theme(panel.grid.major = element_blank(), panel.grid.minor = element_blank())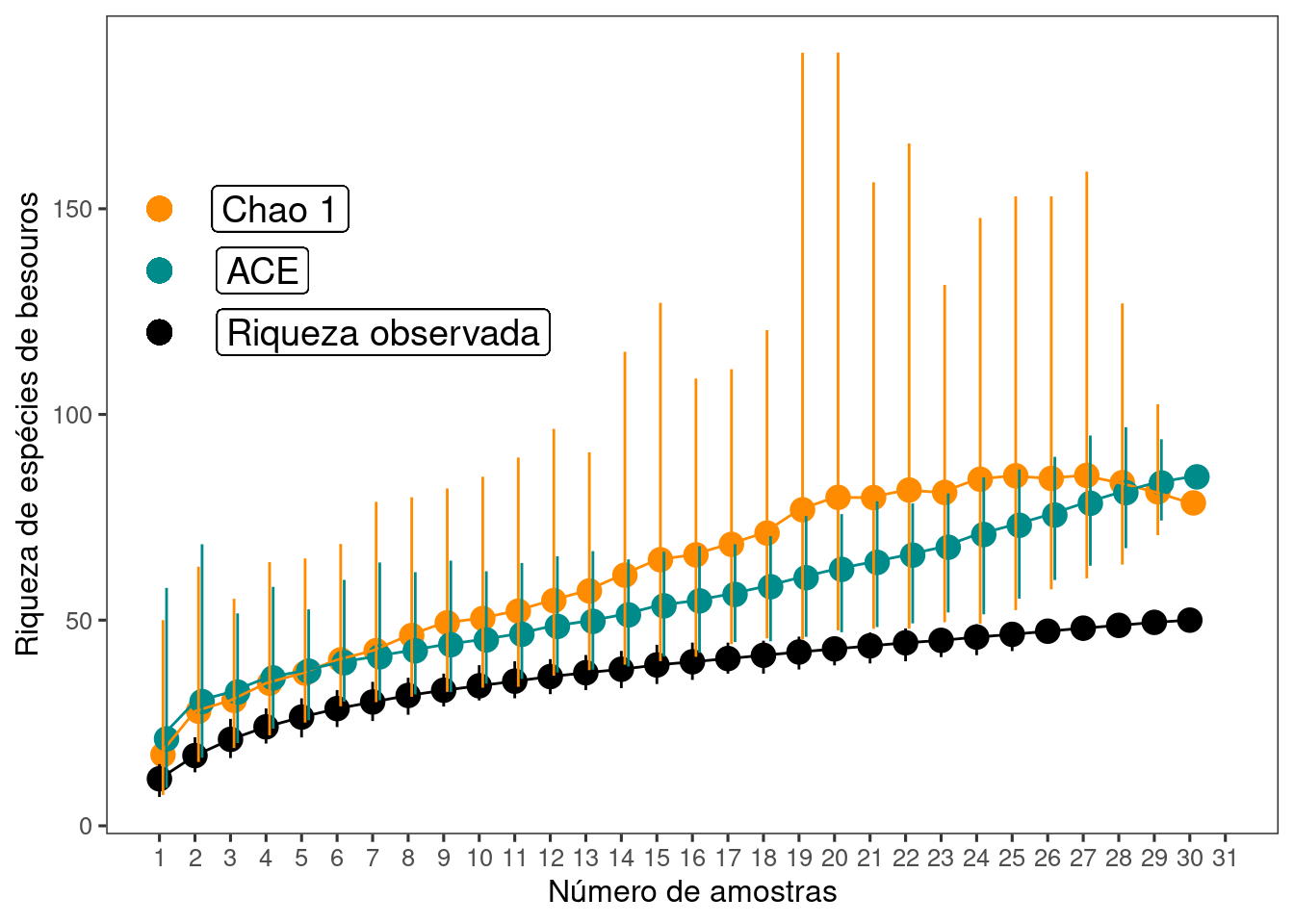
11.2
Utilize o mesmo conjunto de dados do exercício anterior. Calcule os estimadores de riqueza - Jackknife 1 e bootstrap. Faça um gráfico contendo a riqueza observada e os dois estimadores de riqueza. Qual a sua interpretação sobre o esforço amostral? Compare com os resultados do exercício anterior que utilizam estimadores baseados na abundância das espécies.
Solução:
# Carregar a planilha com os dados
exercicio_1 <- ecodados::Cap11_exercicio1
# estimadores incidencia
est_inc <- poolaccum(exercicio_1, permutations = 100)
## Preparando os dados para fazer o gráfico
resultados_inc <- summary(est_inc
, display = c("S", "jack1", "boot"))
res_inc <- cbind(resultados_inc$jack1[, 1:4], resultados_inc$boot[, 2:4],
resultados_inc$S[, 2:4])
res_inc <- as.data.frame(res_inc)
colnames(res_inc) <- c("Amostras", "jack1", "j_inferior", "j_superior",
"boot", "B_inferior", "B_superior",
"Riqueza", "R_inferior", "R_superior")
## Gráfico
ggplot(res_inc, aes(y = Riqueza, x = Amostras)) +
geom_point(aes(y = jack1, x = Amostras + 0.1), size = 4,
color = "darkorange", alpha = 1) +
geom_point(aes(y = boot, x = Amostras + 0.2), size = 4,
color = "cyan4", alpha = 1) +
geom_point(aes(y = Riqueza, x = Amostras), size = 4,
color = "black", alpha = 1) +
geom_point(y = 70, x = 1, size = 4, color = "darkorange", alpha = 1) +
geom_point(y = 65, x = 1, size = 4, color = "cyan4", alpha = 1) +
geom_point(y = 60, x = 1, size = 4, color = "black", alpha = 1) +
geom_label(y = 70, x = 4.9, label = "Jackknife 1", size = 5) +
geom_label(y = 65, x = 4.6, label = "Bootstrap", size = 5) +
geom_label(y = 60, x = 6.7, label = "Riqueza observada", size = 5) +
geom_line(aes(y = jack1, x = Amostras), color = "darkorange") +
geom_line(aes(y = boot, x = Amostras), color = "cyan4") +
geom_line(aes(y = Riqueza, x = Amostras), color = "black") +
geom_linerange(aes(ymin = j_inferior, ymax = j_superior,
x = Amostras + 0.1), color = "darkorange") +
geom_linerange(aes(ymin = B_inferior, ymax = B_superior,
x = Amostras + 0.2), color = "cyan4") +
geom_linerange(aes(ymin = R_inferior, ymax = R_superior,
x = Amostras), color = "black") +
scale_x_continuous(limits = c(1, 31), breaks = seq(1, 31, 1)) +
labs (x = "Número de amostras", y = "Riqueza de espécies de besouros") +
theme_bw(base_size = 12) +
theme(panel.grid.major = element_blank(), panel.grid.minor = element_blank())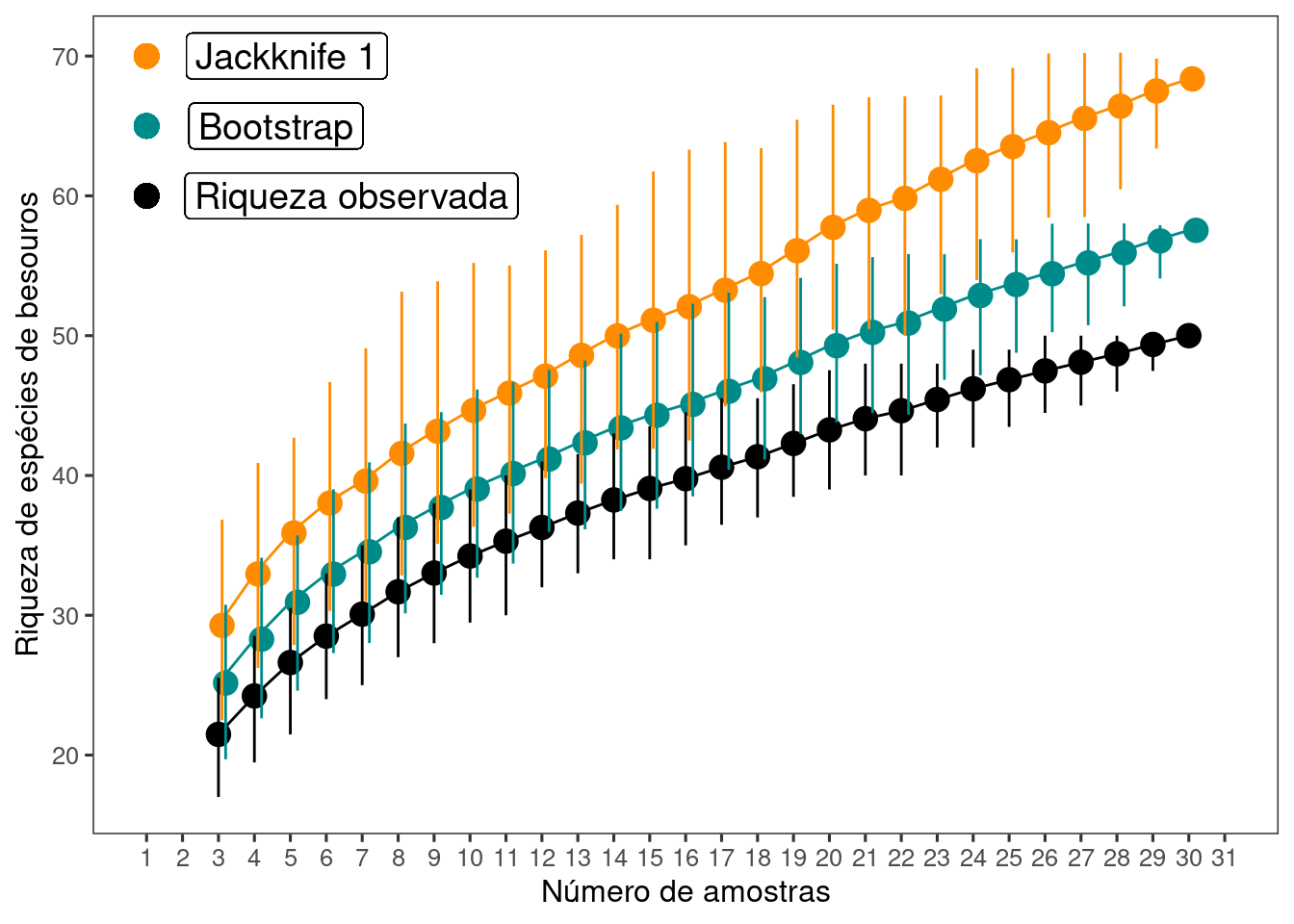
11.3 Vamos refazer o exercício 10 do Capítulo 7 que usa Generalized Least Squares (GLS) para testar a relação da riqueza de anuros em 44 localidades na Mata Atlântica com a precipitação anual. Contudo, ao invés de considerar a riqueza de espécies de anuros observada como variável resposta, iremos utilizar a riqueza extrapolada. Utilize os dados “anuros_composicao” para estimar a riqueza extrapolada e o dados “anuros_ambientais” para acessar os dados de precipitação anual e coordenadas geográficas. Qual a sua interpretação dos resultados utilizando a riqueza observada e extrapolada?
Solução:
# Carregar a planilha com os dados
exercicio_3 <- ecodados::anuros_composicao
# Verificar a comunidade com maior abundãncia.
abund_max <- max(colSums(exercicio_3))
# Calcular a riqueza extrapolada de espécies para todas as comunidades
# considerando a maior abundância.
resultados_extrapolacao <- iNEXT(exercicio_3, q = 0,
datatype = "abundance",
endpoint = abund_max)
# Loop para determinar a riqueza extrapolada para as 44 localidades
resultados_comunidades_ext <- data.frame()
riqueza_extrapolada <- c()
for (i in 1:44){
resultados_comunidades_ext <- data.frame(resultados_extrapolacao$iNextEst[i])
riqueza_extrapolada[i] <- resultados_comunidades_ext[40, 4]
}
# carregando o data frame com todas as variáveis
exercicio_3_1 <- ecodados::anuros_ambientais
# Criando um data frame com a riqueza extrapolada, precipitação anual,
# latitude e longitude
dados_combinado_ext <- data.frame(riqueza_extrapolada, exercicio_3_1[,c(3,5,6)])
## Modelo gls sem estrutura espacial
no_spat_gls <- gls(riqueza_extrapolada ~ Prec_anual, dados_combinado_ext, method = "REML")
## Covariância esférica
espher_model <- gls(riqueza_extrapolada ~ Prec_anual, dados_combinado_ext,
corSpher(form = ~Latitude + Longitude, nugget = TRUE))
## Covariância exponencial
expon_model <- gls(riqueza_extrapolada ~ Prec_anual, dados_combinado_ext,
corExp(form = ~Latitude + Longitude, nugget = TRUE))
## Covariância Gaussiana
gauss_model <- gls(riqueza_extrapolada ~ Prec_anual, dados_combinado_ext,
corGaus(form = ~Latitude + Longitude, nugget = TRUE))
## Covariância linear
cor_linear_model <- gls(riqueza_extrapolada ~ Prec_anual, dados_combinado_ext,
corLin(form = ~Latitude + Longitude, nugget = TRUE),
control = glsControl(opt='optim', msVerbose = F))
## Covariância razão quadrática
ratio_model <- gls(riqueza_extrapolada ~ Prec_anual, dados_combinado_ext,
corRatio(form = ~Latitude + Longitude, nugget = TRUE))
## Seleção de modelos
aic_fit <- AIC(no_spat_gls, espher_model, cor_linear_model, expon_model,
gauss_model,ratio_model)
aic_fit %>% arrange(AIC)
#> df AIC
#> no_spat_gls 3 338.8380
#> gauss_model 5 339.6672
#> ratio_model 5 339.6853
#> expon_model 5 340.3431
#> espher_model 5 342.8380
#> cor_linear_model 5 342.8489
## Gráfico
plot(residuals(espher_model, type = "normalized") ~ fitted(espher_model))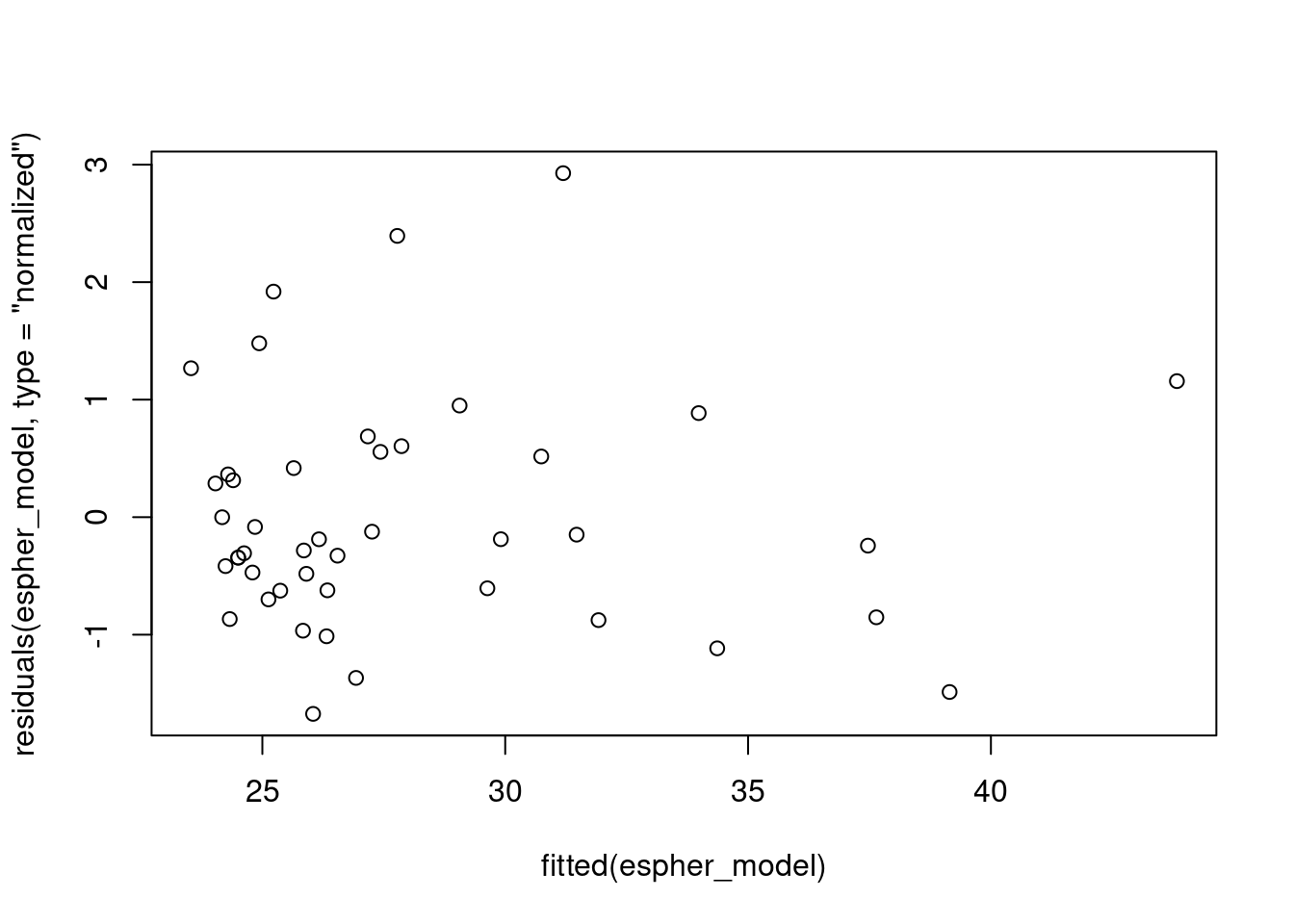
## Varigrama
espher_model_variog <- Variogram(espher_model, form = ~Latitude + Longitude,
resType = "normalized")
plot(espher_model_variog, main = "Variograma com o modelo de Covariância Esférica")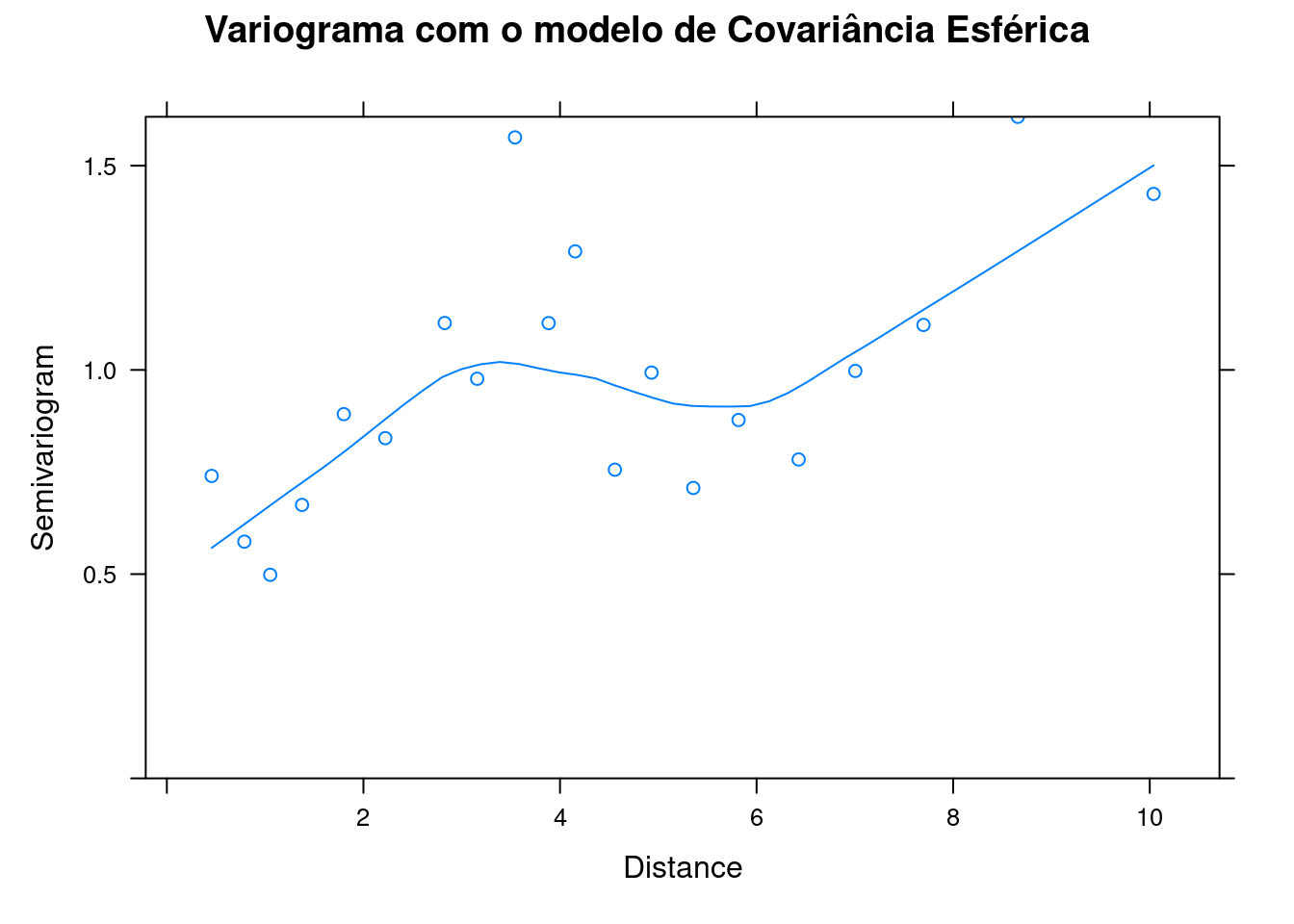
## Resumo dos modelos
summary(espher_model)$tTable
#> Value Std.Error t-value p-value
#> (Intercept) 3.7004741 8.319750795 0.4447818 0.658761200
#> Prec_anual 0.0173344 0.005831002 2.9727995 0.004869827
summary(no_spat_gls)$tTable
#> Value Std.Error t-value p-value
#> (Intercept) 3.7004741 8.319750757 0.4447818 0.658761200
#> Prec_anual 0.0173344 0.005831002 2.9727995 0.004869827