Cap. 9 - Análises Multivariadas
# Pacotes necessários
library(vegan)
library(mvabund)
library(MASS)
library(FactoMineR)
library(ecodados)
library(spdep)
library(adespatial)9.1 Utilize os dados mite do pacote vegan para testar o efeito de variáveis ambientais sobre a composição de espécies de ácaros utilizando as seguintes análises: RDA, RDAp (combinada com MEM), dbRDA e PERMANOVA. Após realizar as cinco análises, responda às seguintes perguntas?
- Quais são as variáveis ambientais (mite.env) mais importantes para a composição de ácaros em cada uma das análises?
- Os vetores espaciais obtidos com a análise MEM explicam a variação na composição de espécies? Eles são mais ou menos importantes do que as variáveis ambientais?
- Discuta as diferenças de interpretação entre a RDA, RDAp, dbRDA e PERMANOVA.
Dados necessários:
Solução:
# Matriz padronizada - Hellinger
species.hel <- decostand(x = mite, method = "hellinger")
# verificar se algum local está sem nenhuma espécie
sum(rowSums(species.hel)==0)
#> [1] 0
# verificar se algum espécie não está em nenhuma localidade
sum(colSums(species.hel)==0)
#> [1] 0
# RDA
#*******************************************************
## RDA com dados ambientais
rda.mite <- rda(species.hel ~ ., data = mite.env)
res.axis <- anova.cca(rda.mite, by = "axis")
res.var <- anova.cca(rda.mite, by = "term")
res.axis
#> Permutation test for rda under reduced model
#> Forward tests for axes
#> Permutation: free
#> Number of permutations: 999
#>
#> Model: rda(formula = species.hel ~ SubsDens + WatrCont + Substrate + Shrub + Topo, data = mite.env)
#> Df Variance F Pr(>F)
#> RDA1 1 0.137314 42.6606 0.001 ***
#> RDA2 1 0.024663 7.6624 0.001 ***
#> RDA3 1 0.013824 4.2949 0.048 *
#> RDA4 1 0.011180 3.4734 0.129
#> RDA5 1 0.008297 2.5776 0.374
#> RDA6 1 0.005485 1.7040 0.840
#> RDA7 1 0.002106 0.6544 1.000
#> RDA8 1 0.001893 0.5881 1.000
#> RDA9 1 0.001272 0.3952 1.000
#> RDA10 1 0.000983 0.3055 1.000
#> RDA11 1 0.000570 0.1770 1.000
#> Residual 58 0.186688
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
res.var
#> Permutation test for rda under reduced model
#> Terms added sequentially (first to last)
#> Permutation: free
#> Number of permutations: 999
#>
#> Model: rda(formula = species.hel ~ SubsDens + WatrCont + Substrate + Shrub + Topo, data = mite.env)
#> Df Variance F Pr(>F)
#> SubsDens 1 0.015943 4.9531 0.004 **
#> WatrCont 1 0.112894 35.0738 0.001 ***
#> Substrate 6 0.040068 2.0747 0.002 **
#> Shrub 2 0.019781 3.0728 0.002 **
#> Topo 1 0.018902 5.8725 0.001 ***
#> Residual 58 0.186688
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# dbRDA
#*******************************************************
dbrda.mite <- capscale(species.hel ~ .,
data = mite.env, dist="bray")
dbrda.axis <- anova.cca(dbrda.mite, by = "axis")
dbrda.var <- anova.cca(dbrda.mite, by = "term")
dbrda.axis
#> Permutation test for capscale under reduced model
#> Forward tests for axes
#> Permutation: free
#> Number of permutations: 999
#>
#> Model: capscale(formula = species.hel ~ SubsDens + WatrCont + Substrate + Shrub + Topo, data = mite.env, distance = "bray")
#> Df SumOfSqs F Pr(>F)
#> CAP1 1 4.1328 43.3801 0.001 ***
#> CAP2 1 0.7100 7.4528 0.001 ***
#> CAP3 1 0.3723 3.9080 0.028 *
#> CAP4 1 0.2420 2.5403 0.294
#> CAP5 1 0.1899 1.9930 0.617
#> CAP6 1 0.1531 1.6069 0.822
#> CAP7 1 0.0762 0.7998 1.000
#> CAP8 1 0.0640 0.6713 1.000
#> CAP9 1 0.0432 0.4535 1.000
#> CAP10 1 0.0378 0.3971 1.000
#> CAP11 1 0.0329 0.3449 0.998
#> Residual 58 5.5257
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
dbrda.var
#> Permutation test for capscale under reduced model
#> Terms added sequentially (first to last)
#> Permutation: free
#> Number of permutations: 999
#>
#> Model: capscale(formula = species.hel ~ SubsDens + WatrCont + Substrate + Shrub + Topo, data = mite.env, distance = "bray")
#> Df SumOfSqs F Pr(>F)
#> SubsDens 1 0.4291 4.5041 0.002 **
#> WatrCont 1 3.4806 36.5343 0.001 ***
#> Substrate 6 1.0988 1.9222 0.007 **
#> Shrub 2 0.5494 2.8835 0.006 **
#> Topo 1 0.4963 5.2091 0.001 ***
#> Residual 58 5.5257
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# PERMANOVA
#*******************************************************
species.dis <- vegdist(species.hel, "bray")
permanova.mite <- adonis(species.hel~., data = mite.env, method = "bray")
permanova.mite
#>
#> Call:
#> adonis(formula = species.hel ~ ., data = mite.env, method = "bray")
#>
#> Permutation: free
#> Number of permutations: 999
#>
#> Terms added sequentially (first to last)
#>
#> Df SumsOfSqs MeanSqs F.Model R2 Pr(>F)
#> SubsDens 1 0.4017 0.4017 5.696 0.04059 0.001 ***
#> WatrCont 1 3.4749 3.4749 49.278 0.35117 0.001 ***
#> Substrate 6 0.9460 0.1577 2.236 0.09561 0.001 ***
#> Shrub 2 0.5100 0.2550 3.616 0.05154 0.002 **
#> Topo 1 0.4726 0.4726 6.701 0.04776 0.003 **
#> Residuals 58 4.0899 0.0705 0.41333
#> Total 69 9.8950 1.00000
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# RDAp
#*******************************************************
# Gerar vetores espaciais: MEM
mite_knn <- knearneigh(as.matrix(mite.xy), k = 2, longlat = FALSE)
mite_nb <- knn2nb(mite_knn, sym = TRUE)
mite_listw <- nb2listw(mite_nb, style = "W")
mite_MEM <- scores.listw(mite_listw, MEM.autocor = "positive")
mite_candidates <- listw.candidates(mite.xy, nb = c("gab", "mst", "dnear"),
weights = c("binary", "flin"))
W_sel_mite <- listw.select(species.hel, mite_candidates, MEM.autocor = "positive",
p.adjust = TRUE, method = "FWD")
#> Procedure stopped (alpha criteria): pvalue for variable 13 is 0.054000 (> 0.050000)
#> Procedure stopped (alpha criteria): pvalue for variable 14 is 0.054000 (> 0.050000)
#> Procedure stopped (alpha criteria): pvalue for variable 14 is 0.069000 (> 0.050000)
#> Procedure stopped (alpha criteria): pvalue for variable 16 is 0.073000 (> 0.050000)
#> Procedure stopped (adjR2thresh criteria) adjR2cum = 0.451035 with 11 variables (> 0.445310)
#> Procedure stopped (alpha criteria): pvalue for variable 12 is 0.052000 (> 0.050000)
mite_sel_MEM <- as.data.frame(W_sel_mite$best$MEM.select)
rownames(mite_sel_MEM) <- rownames(mite.xy)
mite_pred_vars <- data.frame(mite.env, mite_sel_MEM)
names(mite_sel_MEM)
#> [1] "MEM4" "MEM2" "MEM1" "MEM9" "MEM3" "MEM8" "MEM31"
#> [8] "MEM7" "MEM17" "MEM13" "MEM6" "MEM5" "MEM11"
names(mite.env)
#> [1] "SubsDens" "WatrCont" "Substrate" "Shrub"
#> [5] "Topo"
rda.p <- rda(species.hel ~
SubsDens+WatrCont+Substrate+Shrub+Topo + # Preditores ambientais
Condition(MEM1 + MEM2 + MEM3 + MEM4), # Preditores espaciais
data = mite_pred_vars)
rda.p.axis <- anova.cca(rda.p, by = "axis")
rda.p.var <- anova.cca(rda.p, by = "term")
rda.p.axis
#> Permutation test for rda under reduced model
#> Forward tests for axes
#> Permutation: free
#> Number of permutations: 999
#>
#> Model: rda(formula = species.hel ~ SubsDens + WatrCont + Substrate + Shrub + Topo + Condition(MEM1 + MEM2 + MEM3 + MEM4), data = mite_pred_vars)
#> Df Variance F Pr(>F)
#> RDA1 1 0.043419 14.6254 0.001 ***
#> RDA2 1 0.017789 5.9921 0.005 **
#> RDA3 1 0.011421 3.8471 0.094 .
#> RDA4 1 0.008586 2.8920 0.310
#> RDA5 1 0.006671 2.2472 0.554
#> RDA6 1 0.002781 0.9366 0.999
#> RDA7 1 0.002383 0.8026 1.000
#> RDA8 1 0.001430 0.4816 1.000
#> RDA9 1 0.001061 0.3574 1.000
#> RDA10 1 0.000778 0.2619 1.000
#> RDA11 1 0.000542 0.1825 1.000
#> Residual 54 0.160312
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
rda.p.var
#> Permutation test for rda under reduced model
#> Terms added sequentially (first to last)
#> Permutation: free
#> Number of permutations: 999
#>
#> Model: rda(formula = species.hel ~ SubsDens + WatrCont + Substrate + Shrub + Topo + Condition(MEM1 + MEM2 + MEM3 + MEM4), data = mite_pred_vars)
#> Df Variance F Pr(>F)
#> SubsDens 1 0.012981 4.3726 0.001 ***
#> WatrCont 1 0.035825 12.0675 0.001 ***
#> Substrate 6 0.033368 1.8733 0.003 **
#> Shrub 2 0.010736 1.8082 0.025 *
#> Topo 1 0.003949 1.3301 0.177
#> Residual 54 0.160312
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Respostas
A) Quais são as variáveis ambientais (mite.env) mais importantes para a composição de ácaros em cada uma das análises?
RDA simples -> todas as variáveis afetaram a composição de espécies, mas a variável WatrCont foi a mais importante (F = 35,07) dbRDA -> todas as variáveis afetaram a composição de espécies, mas a variável WatrCont foi a mais importante (F = 36,53) PERMANOVA -> todas as variáveis afetaram a composição de espécies, mas a variável WatrCont foi a mais importante (F = 35,51) RDAp -> todas as variáveis afetaram a composição de espécies, mas a variável WatrCont foi a mais importante (F = 35,51). Porém, é importante ressaltar que o efeito é bem menor quando incluimos os vetores espaciais.
B) Os vetores espaciais obtidos com a análise MEM explicam a variação na composição de espécies? Eles são mais ou menos importantes do que as variáveis ambientais?
Os vetores espaciais possuem efeito sobre a composição de ácaros, especialmente os MEMs 4, 2, 9, 1, 3, 6, 7, 13 e 31. A partição de variância indica que o valor espacial “puro” é mais importante do que o ambiental “puro”. Porém, a variação ambiental espacialmente estruturada tem maior poder de explicação.
C) Discuta as diferenças de interpretação entre a RDA, RDAp, dbRDA e PERMANOVA.
As análises que não incluem o componente espacial (RDA, dbRDA e PERMANOVA) enfatizam a relevância das variáveis ambientais e não foram capazes de identificar que parte da explicação atribuída à variação ambiental é, de fato, explicada pela estrutura espacial nas variáveis ambientais e na composição de espécies
9.2 Efetue uma análise de agrupamento pela função hclust(). Lembre-se de dar nome ao objeto para poder plotar o dendrograma depois. Utilize a ajuda para encontrar como entrar com os argumentos da função.
- utilizando o método UPGMA e o índice de Bray-Curtis.
- Faça agora o dendrograma com outro índice de dissimilaridade e compare os resultados. São diferentes? No que eles influenciaríam a interpretação do resultado?
Solução:
##trans. numa matriz de dissimilaridade
matriz<-vegdist(mite, method="bray")
matriz1<-hclust(matriz, method="complete")
plot(matriz1)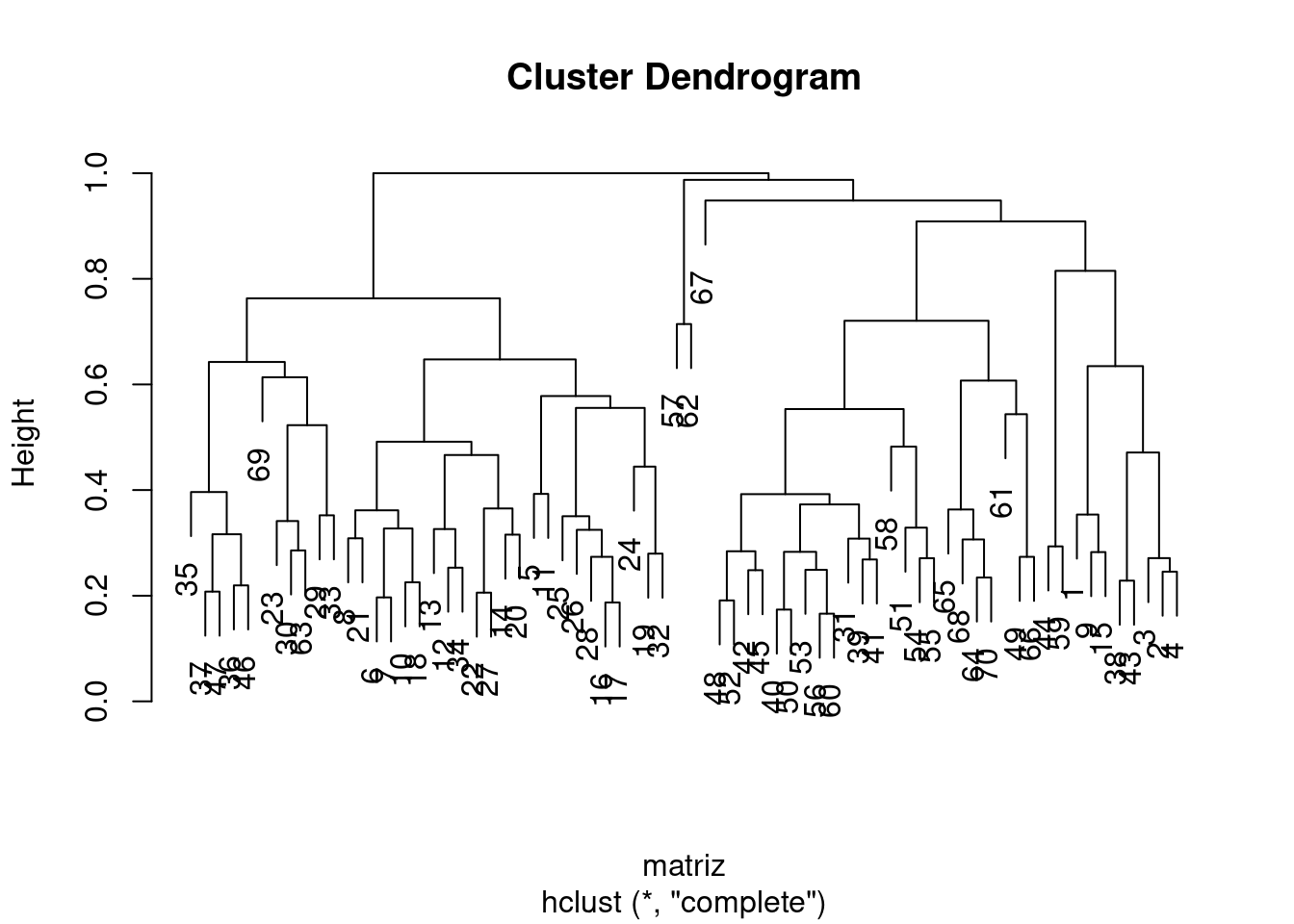
##transforma a matriz com outro índice
outroindice<-vegdist(mite, method="jaccard")
outro<-hclust(outroindice, method="complete")
plot(outro)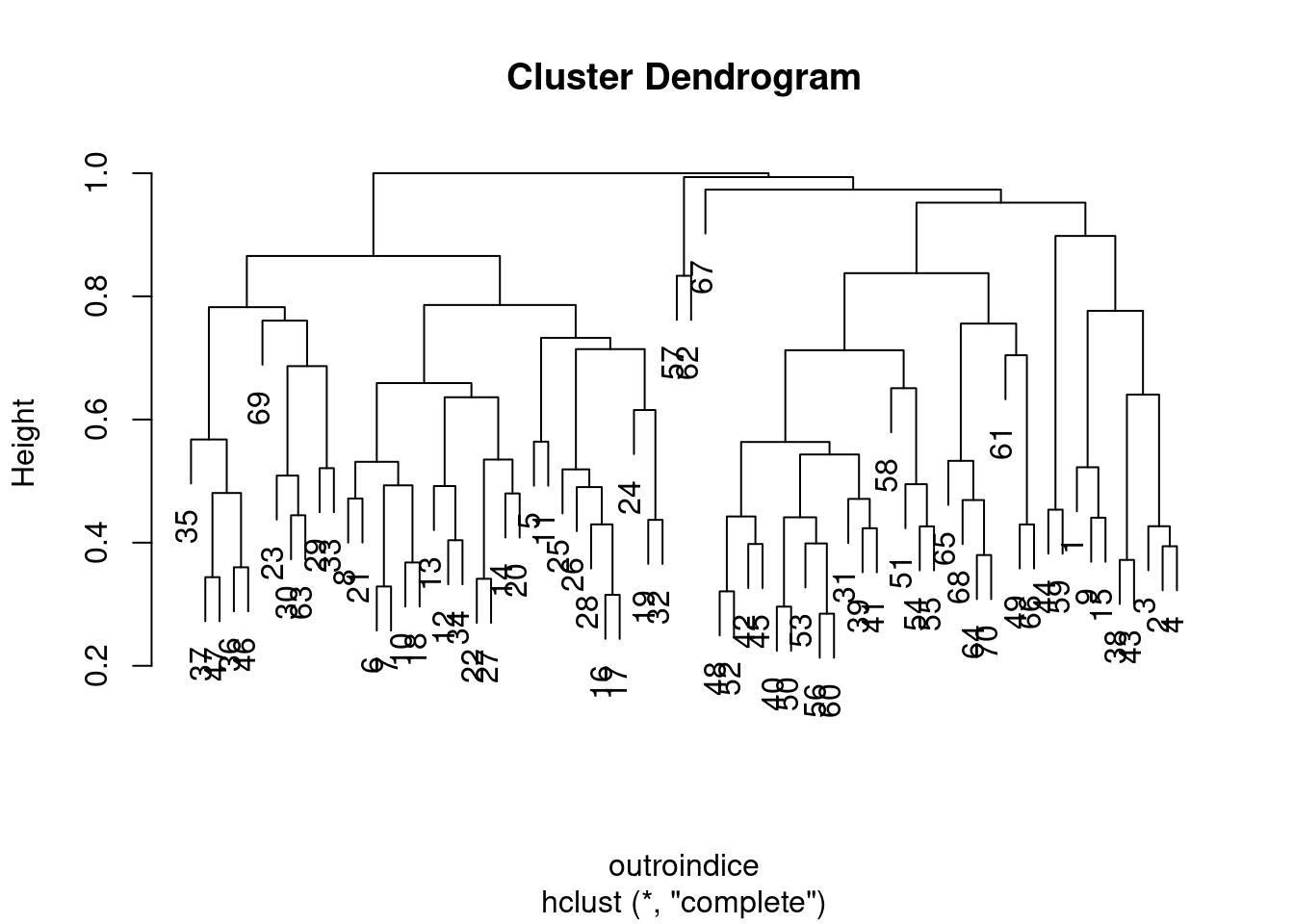
9.3 Na perspectiva de metacomunidades (Leibold et al., 2004), a dispersão dos organismos tem um papel proeminente para entender como as espécies estão distribuídas na natureza. Com o objetivo de testar se a dispersão influencia a composição de espécies de cladóceros e copépodos, e portanto a estrutura da metacomunidade, um pesquisador selecionou dois conjuntos de lagos: em um deles todos os lagos são isolados e no outro os lagos são conectados.
Importe o conjunto de dados lagos do pacote
ecodadose responda a pergunta se o fato de os lagos estarem conectados ou não influencia a composição de espécies desses microcrustáceos. Utilize métodos baseados em modelos que você aprendeu ao longo do capítulo para modelar a abundância multivariada.Faça um plot mostrando a abundância relativa das espécies com maior abundância e veja se elas são diferentes entre os tipos lagos. Combine este resultado com o do item anterior para interpretar o resultado final.
Solução:
#A)
head(ecodados::lagos)
#> sp1 sp2 sp3 sp4 sp5 sp6 sp7 sp8 sp9 sp10 sp11 sp12
#> conect1 5 0 8 5 1 1 0 1 0 5 35 0
#> conect2 4 0 12 37 0 0 0 2 0 0 25 0
#> conect3 8 0 13 0 0 0 0 8 0 0 85 0
#> conect4 21 0 28 28 0 0 0 4 0 0 35 0
#> conect5 23 0 29 0 0 0 0 1 0 1 41 0
#> conect6 0 1 7 7 0 0 0 10 0 25 25 0
#> sp13 sp14 sp15 sp16 sp17 sp18 sp19 sp19.1 sp20 sp21
#> conect1 0 0 0 0 5 0 0 2 0 0
#> conect2 0 0 0 0 0 0 0 2 1 0
#> conect3 0 0 0 0 0 0 0 3 2 0
#> conect4 1 0 0 0 0 0 0 7 0 1
#> conect5 0 0 0 1 7 0 0 9 4 0
#> conect6 0 0 0 0 0 0 0 12 0 0
#> sp22
#> conect1 0
#> conect2 0
#> conect3 0
#> conect4 0
#> conect5 0
#> conect6 0
conec=factor(c(rep(1,8), rep(2,8)),labels=c("conect","isol"))
lagos_abund <- mvabund(lagos)
modelo1 <- manyglm(lagos_abund~conec)
plot(modelo1)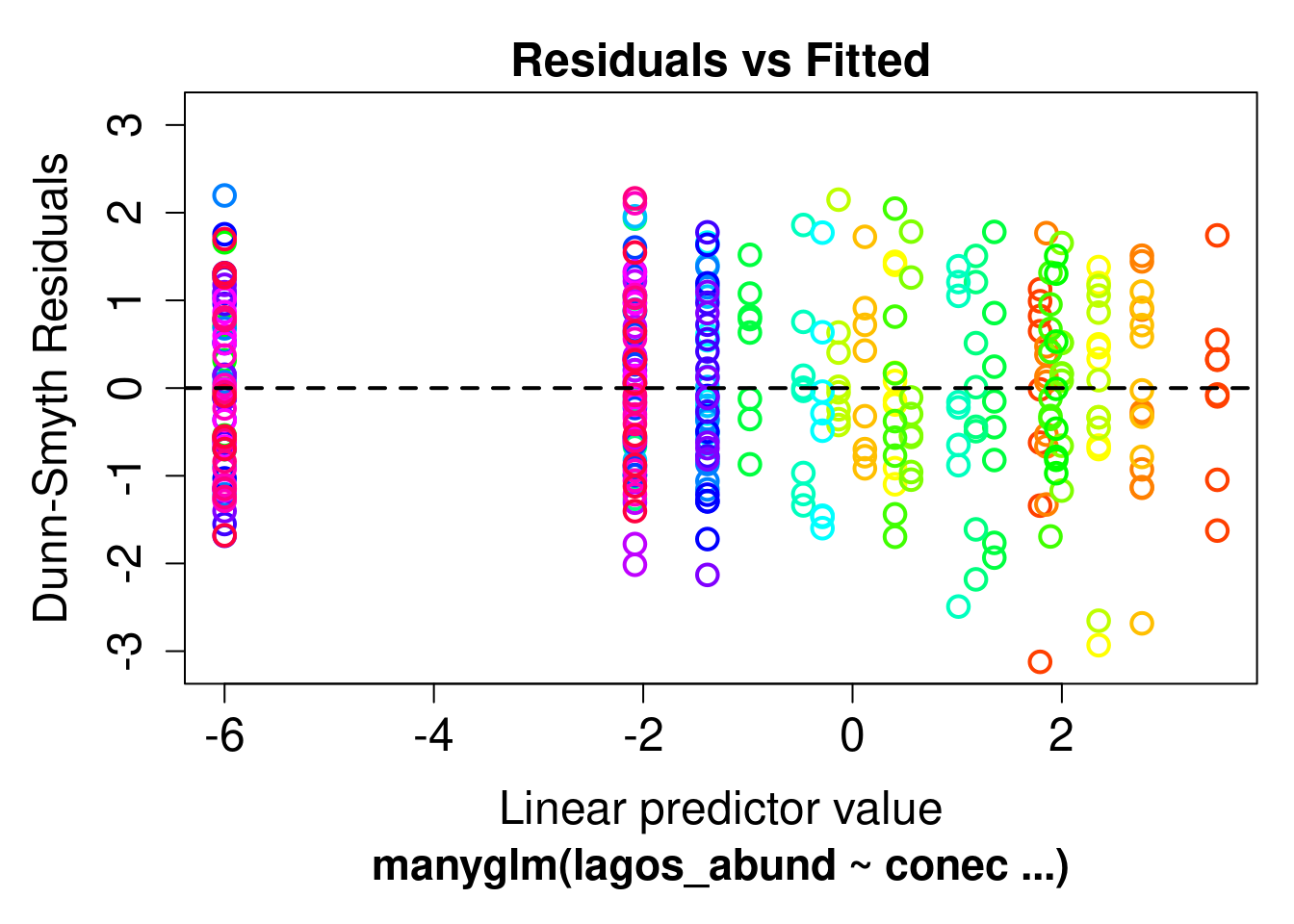
summary(modelo1)
#>
#> Test statistics:
#> wald value Pr(>wald)
#> (Intercept) 22.808 0.001 ***
#> conecisol 9.579 0.001 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Test statistic: 9.579, p-value: 0.001
#> Arguments:
#> Test statistics calculated assuming response assumed to be uncorrelated
#> P-value calculated using 999 resampling iterations via pit.trap resampling (to account for correlation in testing).
#B)
plot(lagos_abund, conec)
#>
#> PIPING TO 1st MVFACTOR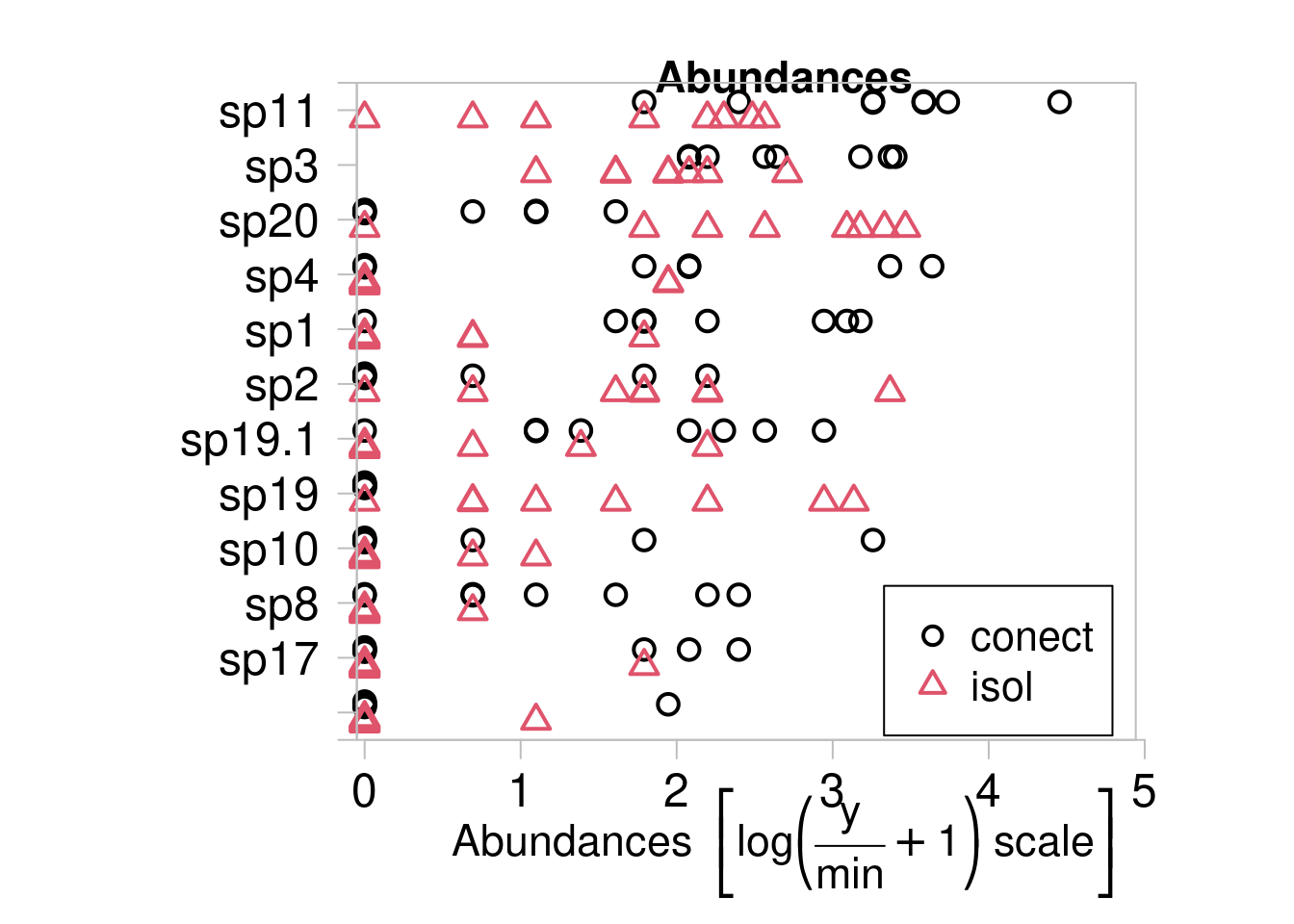
9.4 Carregue o pacote MASS para utilizar os dados crabs. Este conjunto traz medidas morfológicas de dois morfo-tipos da espécie de carangueijo Leptograpsus variegatus coletada em Fremantle, Austrália. Calcule uma PCA e veja se existe uma semelhança morfológica entre os dois morfo-tipos. Lembre-se de dar nome
ao objeto e use a função biplot() para plotar o resultado do teste. Dica: a projeção de um objeto perpendicular à seta do descritor fornece a posição aproximada do objeto ao longo desse descritor. A distância dos objetos no espaço cartesiano reflete a distância euclidiana entre eles.
Solução:
data(crabs)
head(crabs)
#> sp sex index FL RW CL CW BD
#> 1 B M 1 8.1 6.7 16.1 19.0 7.0
#> 2 B M 2 8.8 7.7 18.1 20.8 7.4
#> 3 B M 3 9.2 7.8 19.0 22.4 7.7
#> 4 B M 4 9.6 7.9 20.1 23.1 8.2
#> 5 B M 5 9.8 8.0 20.3 23.0 8.2
#> 6 B M 6 10.8 9.0 23.0 26.5 9.8
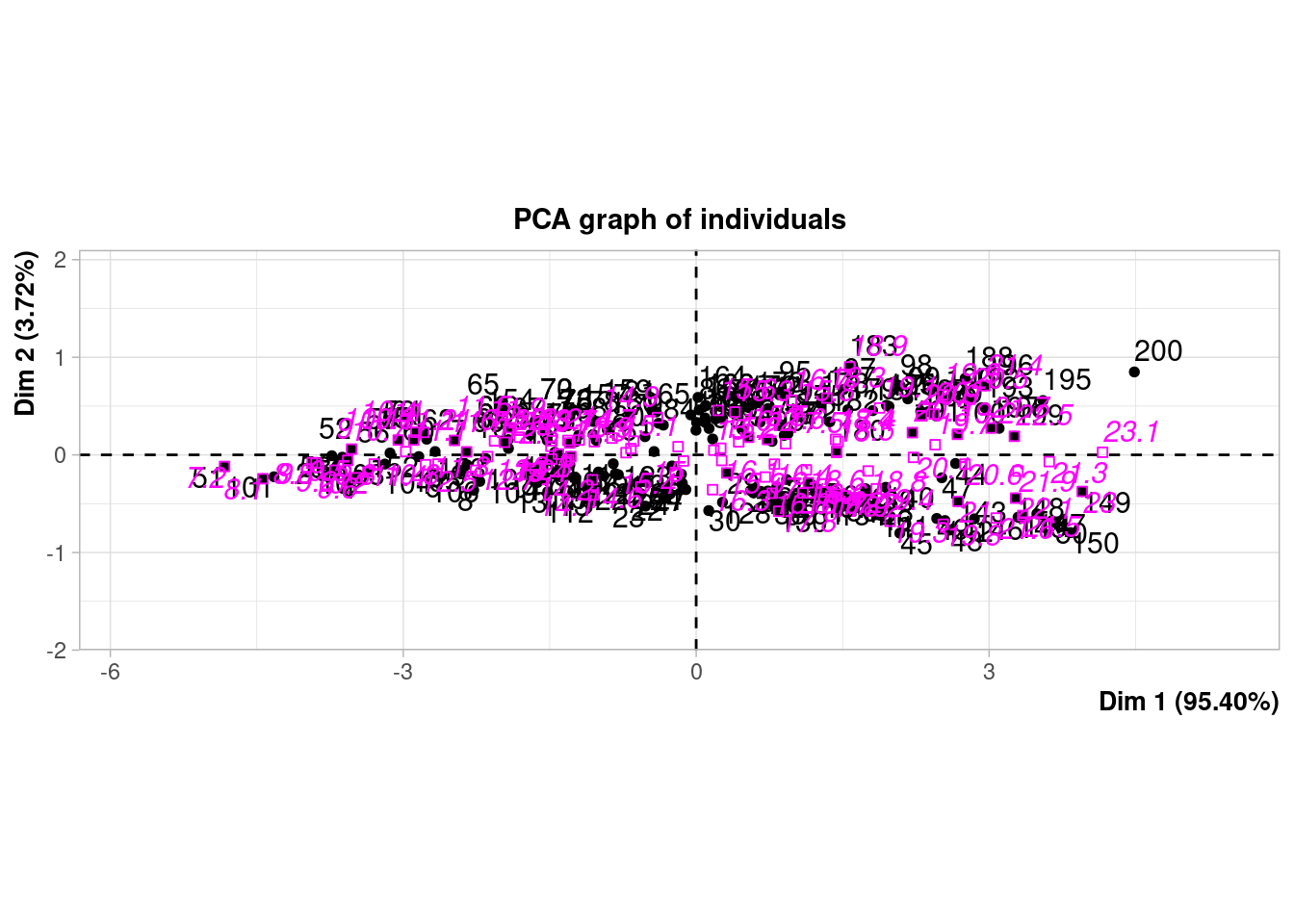
pca_crabs <- PCA(crabs[,4:8], quali.sup = 1, graph = FALSE)
plot(pca_crabs)