Skip to main content

Análises Ecológicas no R: Exercícios e Soluções

Cap. 12 - Diversidade Taxônomica

12.1 Carregue os dados - anuros_composicao - que está no pacote ecodados. Este conjunto de dados representa a abundância de 211 espécies de anuros coletados em 44 localidades na Mata Atlântica. Calcule a riqueza de espécies para cada comunidade e os índices de Margalef, Menhinich, Shannon-Wiener, Gini-Simpson e Equitabilidade de Pielou. Salve todos os resultados em novo data frame. Faça uma gráfico usando o função ggpairs para ver a correlação entre as métricas. Qual a sua interpretação sobre os resultados?

Solução:

# Carregar a planilha com os dados
exercicio_1 <- ecodados::anuros_composicao

# Transpor o data frame para as espécies ficarem nas colunas e as localidades nas linhas
exercicio_1_t <- data.frame(t(exercicio_1))

## Calculando a riqueza observada de espécies para cada comunidade
Riqueza <- specnumber(exercicio_1_t)

## Calculando o Índice de Margalef para cada comunidade
Margalef <- round((Riqueza - 1)/log(apply(exercicio_1_t, 1, sum)), 2)

## Calculando o Índice de Menhinick para cada comunidade
Menhinick <- round(Riqueza/sqrt(apply(exercicio_1_t, 1, sum)), 2)

## Calculando o Índice de Shannon-Wiener para cada comunidade
Shannon <- round(diversity(exercicio_1_t, index = "shannon", MARGIN = 1), 2)

## Calculando o Índice de Gini-Simpson para cada comunidade
Gini_Simpson <- round(diversity(exercicio_1_t, index = "simpson", MARGIN = 1), 2)

## Calculando o Índice de Equitabilidade de Pielou para cada comunidade
Pielou <- round(Shannon/log(Riqueza), 2)

# Criando data frame
resultados <- data.frame(Riqueza, Margalef, Menhinick, Shannon, Gini_Simpson, Pielou)

# Gráfico
ggpairs(resultados, upper = list(continuous = wrap("cor", size = 4))) +
    tema_livro()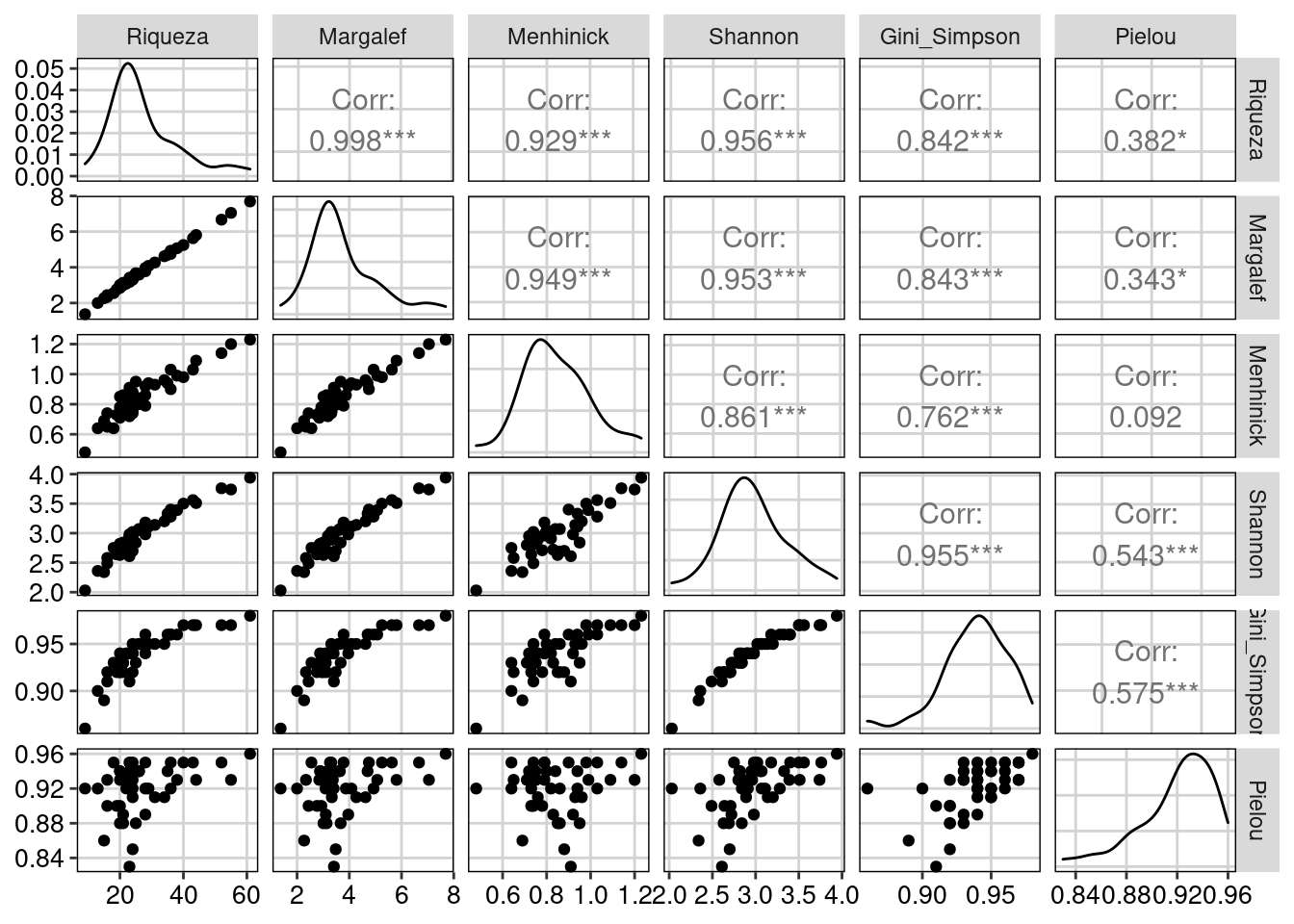

12.2 Usando os resultados anteriores, selecione as duas comunidades com os maiores e menores valores de Shannon-Wiener. Em seguida, faça um Diagrama de Whittaker. Por fim, interprete as curvas considerando as curvas teóricas (i.e., geométrica, broken-stick, etc.) descritas nos livros de ecologia.

Solução:

# Usando os resultados no exercício anterior, vamos verificar quais são as comunidades com maiores e menores valores de Shannon-Wienner
order(resultados$Shannon)
#>  [1] 43 37 12  4 41  1 16 38 19 11 22 44 20 13 10 29 17 24
#> [19] 42  8 15 25 31  7  5 14 18  3 21 39 40 32 30 34 33 27
#> [37] 36  9  2 35 26  6 28 23

# AS comunidades com maiores valores estão nas linhas 6 e 23 e as comunidades com menores valores nas linhas 43 e 37.
rank_com6 <- rankabundance(exercicio_1_t[6, exercicio_1_t[6,] > 0])
rank_com23 <- rankabundance(exercicio_1_t[23, exercicio_1_t[23,] > 0])
rank_com43 <- rankabundance(exercicio_1_t[43, exercicio_1_t[43,] > 0])
rank_com37 <- rankabundance(exercicio_1_t[37, exercicio_1_t[37,] > 0])

## Gráfico
rankabunplot(rank_com6, scale = "logabun", pch = 19, specnames = NULL, 
             col = "darkorange")
rankabunplot(rank_com23, scale = "logabun", pch = 19, specnames = NULL,
             addit = TRUE, col = "red")
rankabunplot(rank_com43, scale = "logabun", pch = 19, specnames = NULL,
             addit = TRUE, col = "cyan4" )
rankabunplot(rank_com37, scale = "logabun", pch = 19, specnames = NULL,
            addit = TRUE, col = "darkblue" )
legend(20, 8, legend = c("Comunidade 6", "Comunidade 23", 
                         "Comunidade 43", "Comunidade 37"),
       col = c("darkorange", "red", "cyan4", "darkblue"), lty = 1, lwd = 3, 
       cex = 1.2, box.lty = 0)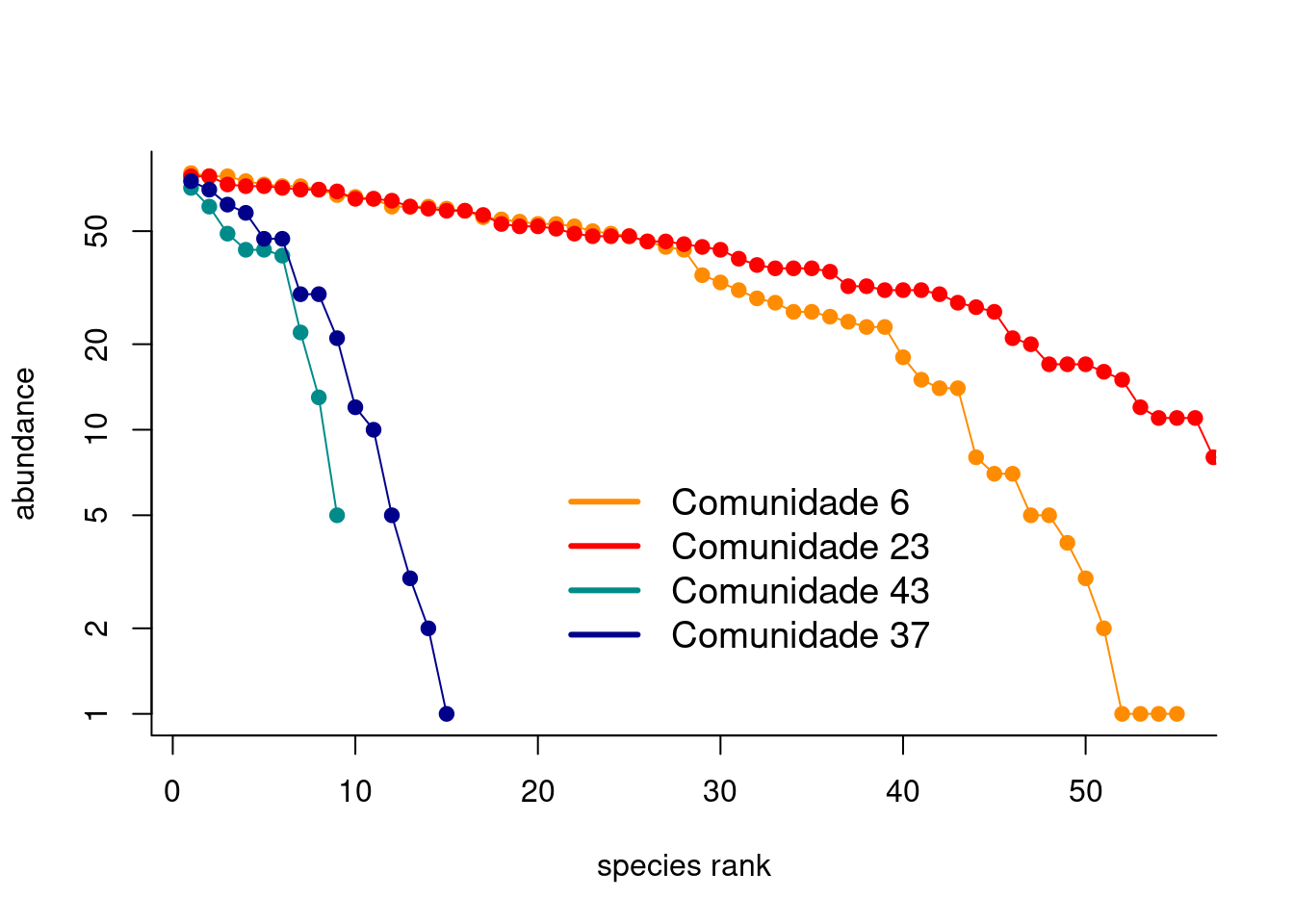

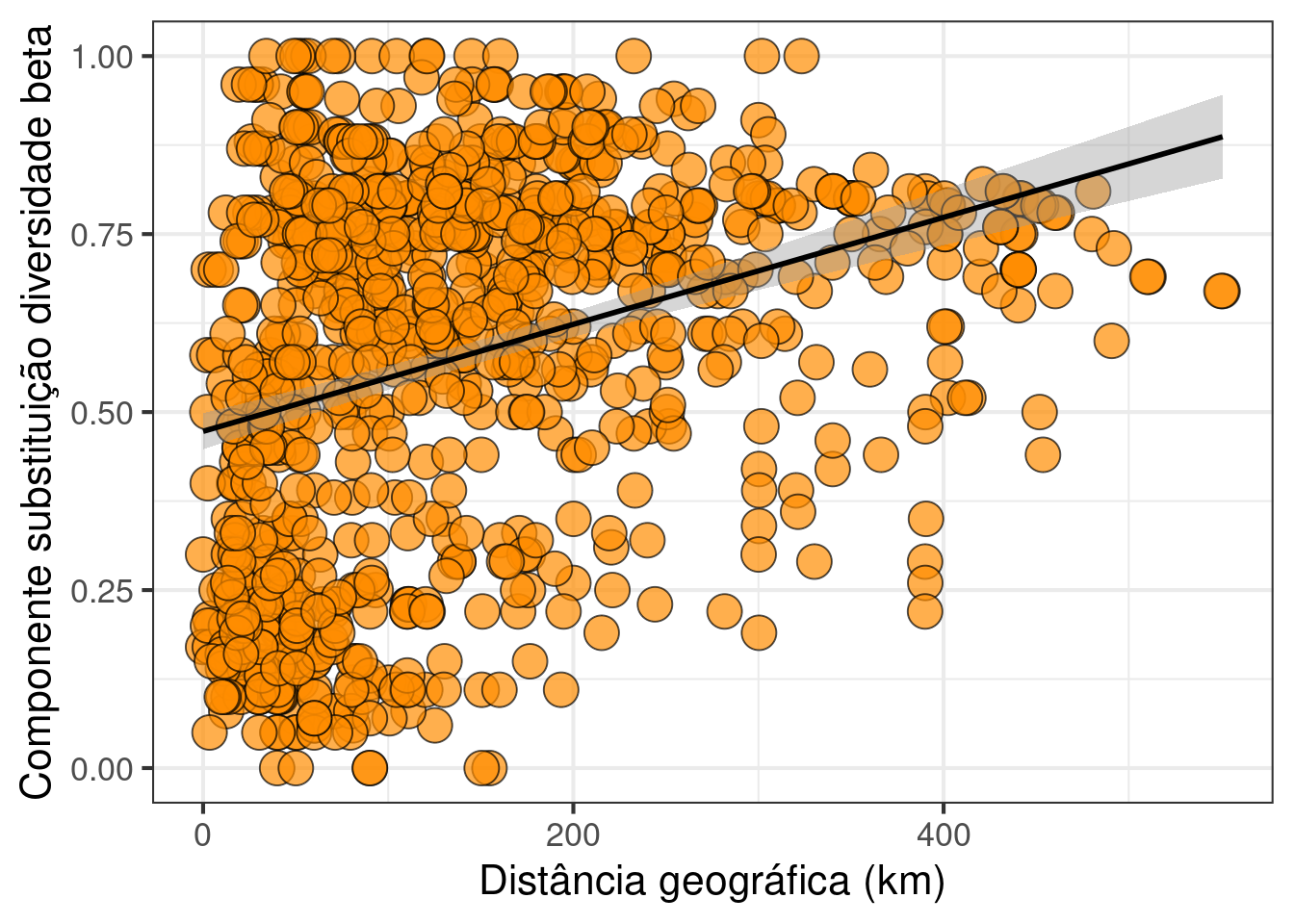
12.3 Usando os dados - anuros_composicao - calcule a partição da diversidade beta considerando os dados de abundância e presença e ausência. a) Faça um gráfico boxplot com os resultados. Discuta se os resultados usando abundância ou presença e ausência são congruentes ou discrepantes. b) Calcule a distância geográfica (use a planilha anuros_ambientais) entre as localidaes (use a Distância euclidiana). Em seguida, faça uma análise de regressão para verificar se as localidades que estão próximas apresentam maior similaridade na composição de espécies (use componente turnover - Bsim) do que as comunidades que estão distantes (e.g., Decaimento da similaridade).

Solução:

# Carregar a planilha com os dados
anuros <- ecodados::anuros_composicao

# Transpor o data frame 
anuros_t <- data.frame(t(anuros))

## Transformando dados em presencia e ausência.
anuros_PA <- decostand(anuros_t, method = "pa")

## Diversidade beta presença e ausência
resultado_PA <- beta.pair(anuros_PA, index.family = "sorensen")

## Diversidade beta abundância
resultado_Abund <- beta.pair.abund(anuros_t, index.family = "bray")

## Criando data frame com os resultados
diver_beta <- c(round(as.numeric(resultado_PA$beta.sor), 2),
                            round(as.numeric(resultado_PA$beta.sim), 2),
                            round(as.numeric(resultado_PA$beta.sne), 2),
                            round(as.numeric(resultado_Abund$beta.bray), 2),
                            round(as.numeric(resultado_Abund$beta.bray.bal), 2),
                            round(as.numeric(resultado_Abund$beta.bray.gra), 2))

Componentes <- rep(c("Bsor", "Bsim", "Bnes", "BBray", "BBray_bal", "BBray_gra"),
             each = 946)
Dados <- rep(c("Incidencia", "Abundância"),
             each = 2838)

data_frame <- data.frame(diver_beta, Componentes, Dados)

# Reordenando os componentes para melhorar visualização no gráfico
data_frame$Componentes <- factor(data_frame$Componentes , levels=c("Bsor", "Bsim", "Bnes", 
                                           "BBray", "BBray_bal", "BBray_gra"))

## Gráfico
ggplot(data_frame, aes(y = diver_beta , x = Componentes, fill = Dados)) + 
  geom_boxplot() +
  theme_bw(base_size = 16) +
  geom_jitter(size = 0.3, width = 0.05) +
  labs( x = "Componentes diversidade beta", y = "Dissimilaridade")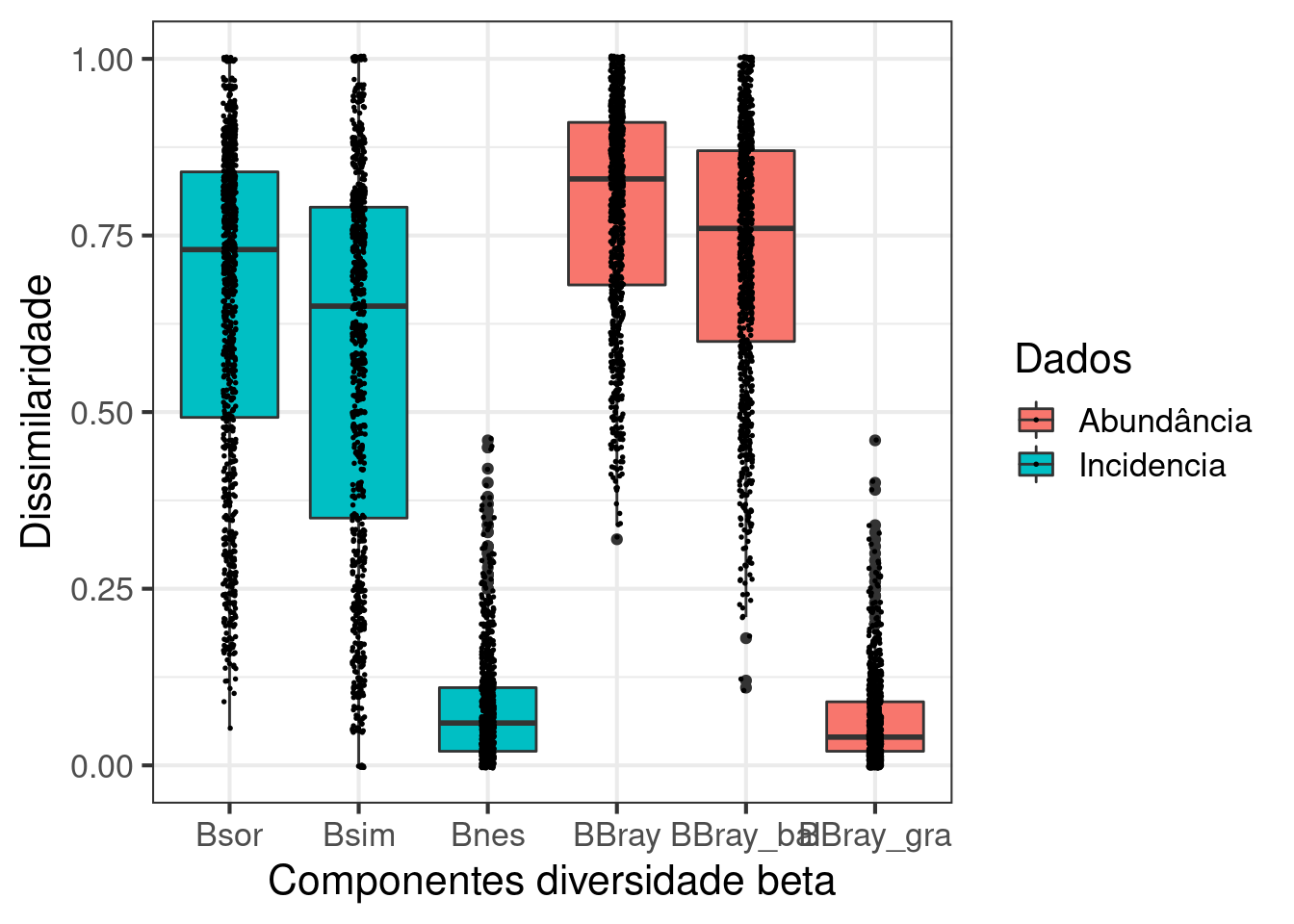


## carregando planilha anuros_ambientais

ambientes <- ecodados::anuros_ambientais

## Distância euclidiana
distancia <- vegdist(ambientes[,c(6,7)], "euclidean")

## criar data frame

dados <- data.frame(round(as.numeric(resultado_PA$beta.sim), 2), 
                    round(as.numeric(distancia), 2))

colnames(dados) <- c("Bsim", "distancia")

## Regressão - Contudo essa não é a melhor análise porque os índices de 
# diversidade beta apresenta um platô.
regr <- lm (dados$Bsim ~ dados$distancia)
summary(regr)
#> 
#> Call:
#> lm(formula = dados$Bsim ~ dados$distancia)
#> 
#> Residuals:
#>      Min       1Q   Median       3Q      Max 
#> -0.58919 -0.21205  0.03911  0.19848  0.50133 
#> 
#> Coefficients:
#>                  Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)     0.4729768  0.0129279   36.59   <2e-16 ***
#> dados$distancia 0.0075119  0.0007092   10.59   <2e-16 ***
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 0.2472 on 944 degrees of freedom
#> Multiple R-squared:  0.1062, Adjusted R-squared:  0.1053 
#> F-statistic: 112.2 on 1 and 944 DF,  p-value: < 2.2e-16

## Gráfico
ggplot(data = dados, aes(x = distancia*10, y = Bsim)) + 
  labs(x = "Distância geográfica (km)", y = "Componente substituição diversidade beta") +
  geom_point(size = 6, shape = 21, fill = "darkorange", alpha = 0.7) +
  theme(legend.position = "none") +
  geom_smooth(method = lm, se = TRUE, color = "black") +
  theme_bw(base_size = 16)