Cap. 14 - Diversidade Funcional
14.1 Utilize os dados “aviurba” do pacote ade4 para testar o efeito de variáveis ambientais na dispersão (FDis) e regularidade funcional (FEve). Utilize modelos lineares (lm) para testar quais variáveis ambientais são as mais importantes para a dispersão e regularidade funcional. Além disso, faça um boxplot comparando os valores de FDis e FEve entre as categorias das variáveis ambientais mais relevantes.
Solução:
# Pacotes e dados
library(ade4)
library(FD)
library(ggplot2)
library(tidyverse)
library(ecodados)
library(gridExtra)
data(aviurba)
com <- aviurba$fau # matriz de composição de espécies
trait <- aviurba$traits # atributos funcionais das espécies
amb <- aviurba$mil # matriz de variáveis ambientais
# 1. Cálculo da diversidade funcional: FDis e FEve
div_fun <- dbFD(trait, com)
#> Species x species distance matrix was not Euclidean. 'sqrt' correction was applied.
#> FRic: Only categorical and/or ordinal trait(s) present in 'x'. FRic was measured as the number of unique trait combinations, NOT as the convex hull volume.
#> FDiv: Cannot be computed when only categorical and/or ordinal trait(s) present in 'x'.
FDis <- div_fun$FDis
FEve <- div_fun$FEve
#. 2. modelos lineares
lm_fdis <- lm(FDis~., data=amb)
anova(lm_fdis)
#> Analysis of Variance Table
#>
#> Response: FDis
#> Df Sum Sq Mean Sq F value Pr(>F)
#> farms 1 0.008631 0.0086311 3.1698 0.08422 .
#> small.bui 1 0.000000 0.0000000 0.0000 0.99665
#> high.bui 1 0.001561 0.0015610 0.5733 0.45434
#> industry 1 0.012983 0.0129830 4.7680 0.03621 *
#> fields 1 0.004193 0.0041926 1.5397 0.22341
#> grassland 1 0.000053 0.0000528 0.0194 0.89007
#> scrubby 1 0.000773 0.0007733 0.2840 0.59767
#> deciduous 1 0.000385 0.0003845 0.1412 0.70948
#> conifer 1 0.000191 0.0001905 0.0700 0.79304
#> noisy 1 0.000386 0.0003859 0.1417 0.70900
#> veg.cover 7 0.020059 0.0028655 1.0524 0.41507
#> Residuals 33 0.089857 0.0027230
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
lm_feve <- lm(FEve~., data=amb)
anova(lm_feve)
#> Analysis of Variance Table
#>
#> Response: FEve
#> Df Sum Sq Mean Sq F value Pr(>F)
#> farms 1 0.00001 0.000007 0.0005 0.981844
#> small.bui 1 0.14651 0.146507 10.7662 0.002446 **
#> high.bui 1 0.00969 0.009687 0.7118 0.404906
#> industry 1 0.00786 0.007860 0.5776 0.452664
#> fields 1 0.03908 0.039083 2.8720 0.099549 .
#> grassland 1 0.00769 0.007686 0.5648 0.457668
#> scrubby 1 0.02200 0.021996 1.6164 0.212489
#> deciduous 1 0.00010 0.000104 0.0076 0.930976
#> conifer 1 0.00192 0.001921 0.1412 0.709495
#> noisy 1 0.04924 0.049236 3.6181 0.065911 .
#> veg.cover 7 0.14969 0.021385 1.5715 0.178578
#> Residuals 33 0.44907 0.013608
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# 3. Para facilitar a construção dos gráficos, podemos criar um data.frame
dat_graf <- data.frame(amb, FDis, FEve)
# 4. Gráficos
dat_graf %>%
ggplot(aes(x = industry, y = FDis, fill = industry)) +
geom_boxplot(width = 0.4, alpha = 0.7)+
scale_fill_manual(values = c("cyan4", "darkorange"))+
labs(x = "Presença de indústrias", y = "Divergência Funcional (FDis)") +
tema_livro() -> g_fdis
dat_graf %>%
ggplot(aes(x = small.bui, y = FDis, fill = small.bui)) +
geom_boxplot(width = 0.4, alpha = 0.7)+
scale_fill_manual(values = c("cyan4", "darkorange"))+
labs(x = "Presença de pequenas construções", y = "Regularidade Funcional (FEve)") +
tema_livro() -> g_feve
grid.arrange(g_fdis, g_feve, nrow = 1)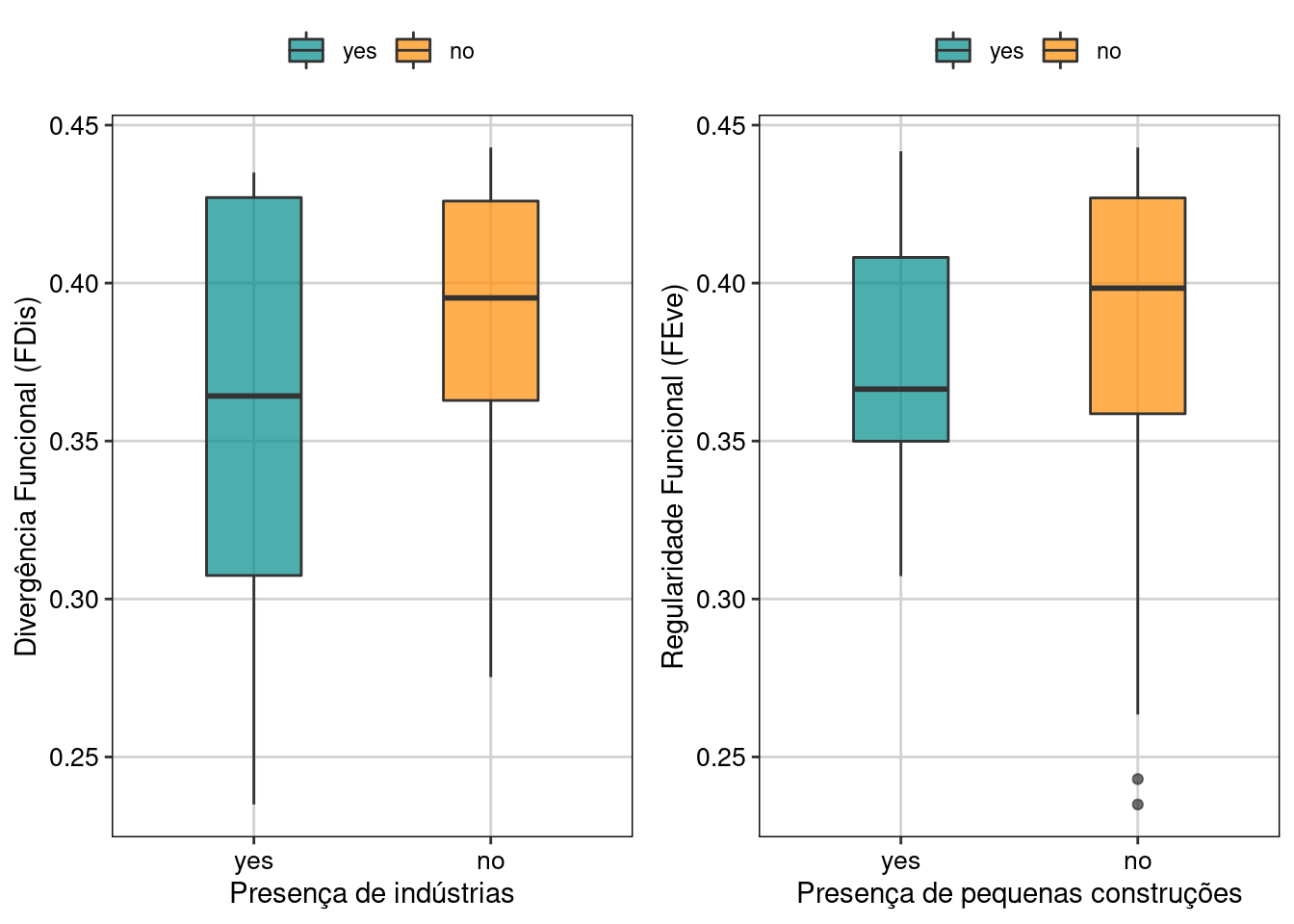
14.2 Utilize os dados “mafragh” do pacote ade4 para teste o efeito da das variáveis “conductivity”, “silt” e “K2O” na diversidade funcional (método de Petchey e Gaston). Utilize modelos lineares (regressão múltipla) para testar a relação entre essas variáveis e discuta (a) qual variável mais importante (se houver) e (b) se as conclusões são coerentes tendo como base os pressupostos dos modelos lineares. Além disso, caso exista alguma relação significativa, faça um gráfico (scatterplot) da relação da variável mais importante e a diversidade funcional.
Solução:
# Pacotes e dados
library(ade4)
library(vegan)
library(ape)
library(picante)
library(ggplot2)
library(tidyverse)
library(ecodados)
data(mafragh)
trait_ma <- mafragh$traits$tabQuantitative # atributos funcionais das espécies
amb_ma <- mafragh$env # matriz de variáveis ambientais
com_ma <- mafragh$flo # matriz de composição de espécies
names(com_ma) <- rownames(trait_ma)
# 1. Cálculo da distância funcional
dis <- vegdist(trait_ma, "euclidean")
# 2. Construção do dendrograma
dendro_ma <- hclust(dis, "average")
# 3. Transformar dendrograma em classe phylo
tree_ma<- as.phylo(dendro_ma)
# 4. Diversidade Funcional de Petchey & Gaston
FD_ma <- pd(com_ma, tree_ma)$PD
#. 5. modelo linear
lm_FD <- lm(FD_ma~Conductivity+`K+`+Silt+K2O, data=amb_ma)
par(mfrow = c(2, 2), oma = c(0, 0, 2, 0))
plot(lm_FD)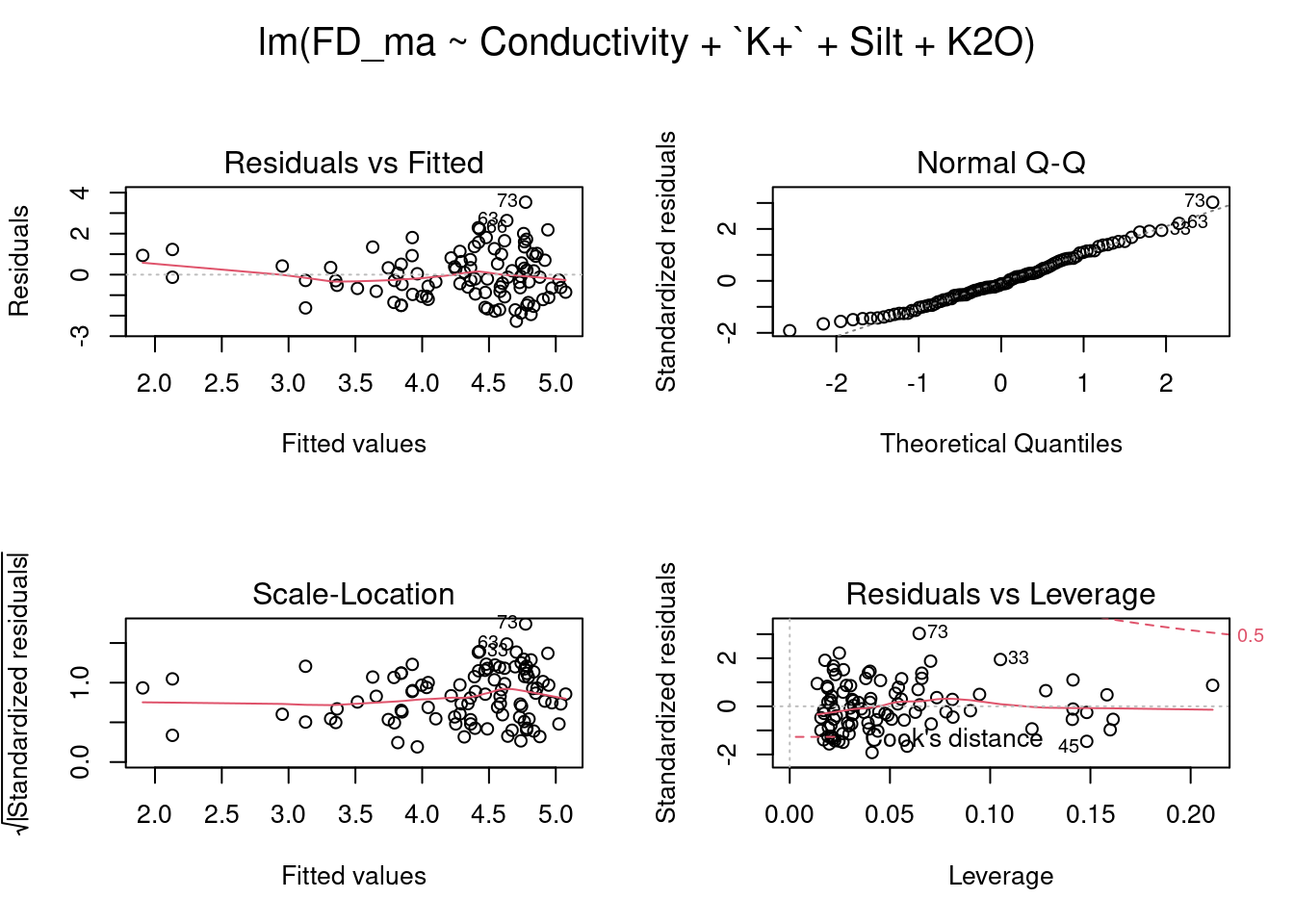
anova(lm_FD) # resultados
#> Analysis of Variance Table
#>
#> Response: FD_ma
#> Df Sum Sq Mean Sq F value Pr(>F)
#> Conductivity 1 2.104 2.104 1.4431 0.2327
#> `K+` 1 35.301 35.301 24.2172 3.76e-06 ***
#> Silt 1 0.232 0.232 0.1592 0.6909
#> K2O 1 0.015 0.015 0.0104 0.9189
#> Residuals 92 134.108 1.458
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# 6. Para facilitar a construção dos gráficos, adicionar FD no data.frame amb_ma
amb_ma$FD <- FD_ma
# 7. Gráfico
amb_ma %>%
ggplot(aes(x = `K+`, y = FD_ma)) +
geom_point(pch = 21, color = "black", fill = "cyan4", size = 3)+
geom_smooth(method = "lm", color = "black") +
labs(x = "Quantidade de K+", y = "Diversidade Funcional (FD)") +
tema_livro() 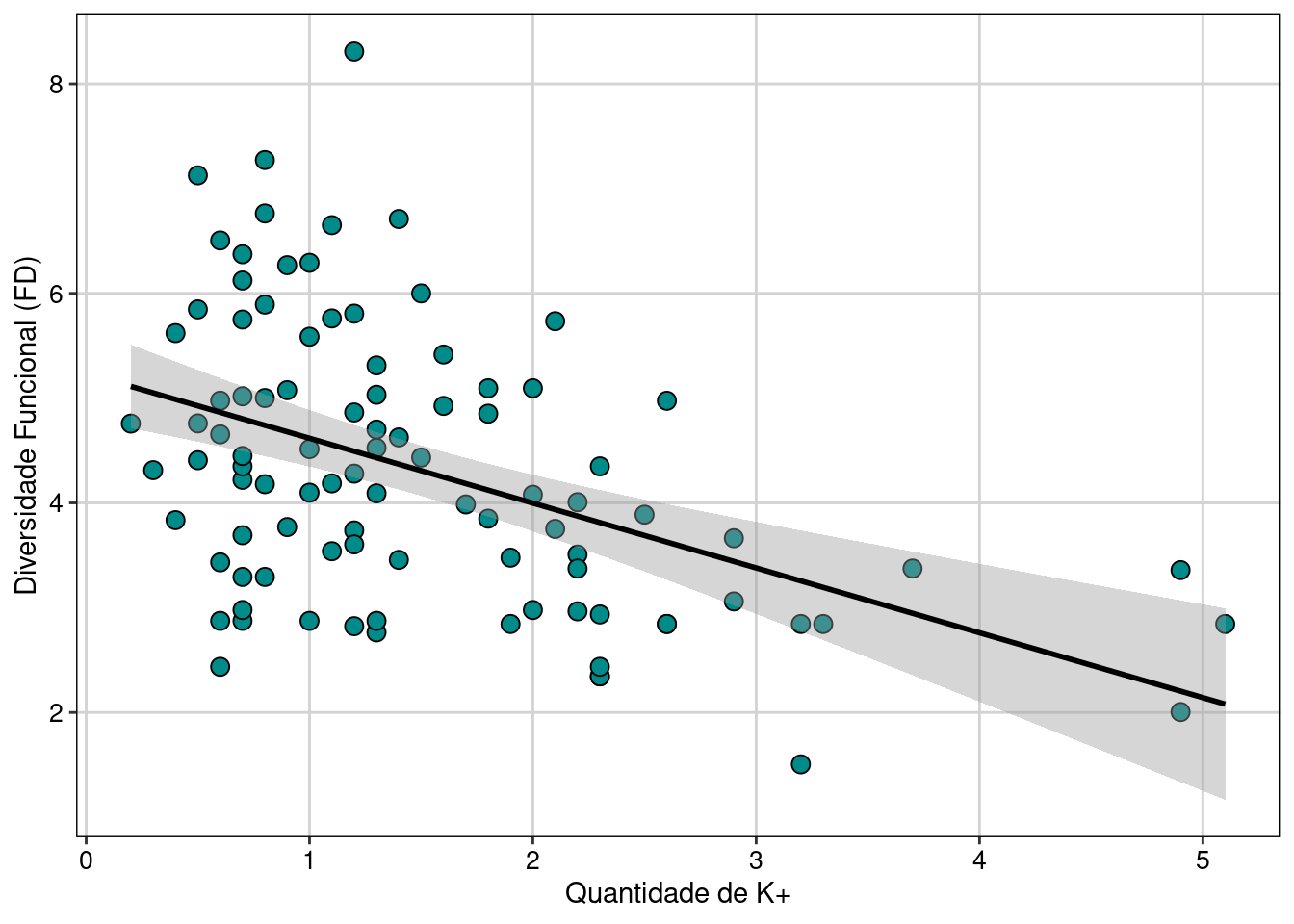
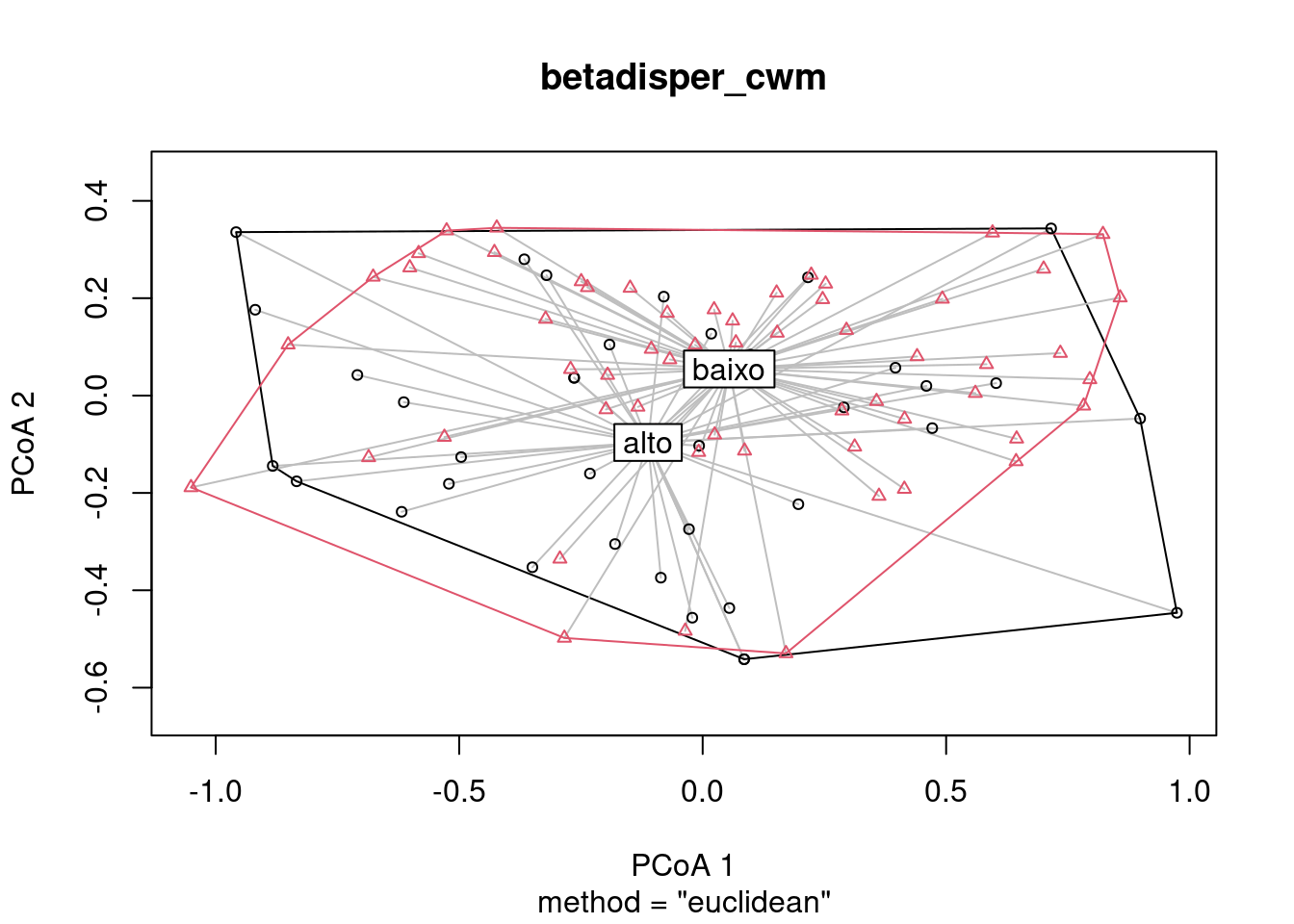
14.3 Utilize os dados “mafragh” do pacote ade4 para comparar a composição filogenética e funcional em áreas com alta e baixa concentração de potássio. Para fazer esta comparação, será necessário transformar a matriz de atributos funcionais e a árvore filogenética em matrizes de distância e, depois, utilizar o CWM para criar uma matriz de localidades por composição funcional ou filogenética. Depois, você poderá usar a matriz CWM para testar potenciais diferenças entre concentrações com PERMANOVA e para visualizar com PCoA.
Solução:
# Pacotes e dados
library(ade4)
library(FD)
library(vegan)
library(ggplot2)
library(tidyverse)
library(ecodados)
data(mafragh)
trait_ma <- mafragh$traits$tabQuantitative # atributos funcionais das espécies
amb_ma <- mafragh$env # matriz de variáveis ambientais
com_ma <- mafragh$flo # matriz de composição de espécies
names(com_ma) <- rownames(trait_ma)
# 1. CWM: Cálculo da composição funcional
cwm_fun <- dbFD(trait_ma, com_ma)$CWM
#> FEVe: Could not be calculated for communities with <3 functionally singular species.
#> FDis: Equals 0 in communities with only one functionally singular species.
#> FRic: To respect s > t, FRic could not be calculated for communities with <3 functionally singular species.
#> FRic: Dimensionality reduction was required. The last PCoA axis (out of 3 in total) was removed.
#> FRic: Quality of the reduced-space representation = 0.8976601
#> FDiv: Could not be calculated for communities with <3 functionally singular species.
# 2. criar uma variável categórica a partir da quantidade de K+
amb_ma$k_cat <- ifelse(amb_ma$`K+` > mean(amb_ma$`K+`), "alto", "baixo")
# 2. PERMANOVA
permanova_cwm <- adonis(cwm_fun ~ k_cat, data = amb_ma)
dis_cwm <- vegdist(cwm_fun, "euclidean")
# 3. Betadisper + gráfico PCoA
betadisper_cwm <- betadisper(dis_cwm, amb_ma$k_cat)
plot(betadisper_cwm)