Cap. 7 - Modelos lineares
# Pacotes necessários
library(ggplot2)
library(ggpubr)
library(lmtest)
library(bbmle)
library(car)
library(ggforce)
library(sjPlot)
library(nlme)
library(dplyr)7.1 Avalie se os indivíduos machos de uma espécie de aranha são maiores do que as fêmeas. Qual a sua interpretação sobre o dimorfismo sexual nesta espécie? Faça um gráfico boxplot usando também a função geom_jitter.Use os dados Cap7_exercicio1 disponível no pacote ecodados.
Solução:
# Carregar dados do pacote ecodados
exercicio_1 <- ecodados::Cap7_exercicio1
# Verificar as premissas do teste
residuos_exercicio1 <- lm(Tamanho ~ Sexo, data = exercicio_1)
# Teste da normalidade dos resíduos
shapiro.test(residuals(residuos_exercicio1))
#>
#> Shapiro-Wilk normality test
#>
#> data: residuals(residuos_exercicio1)
#> W = 0.96586, p-value = 0.4328
# Teste da Homogeneidade da variância dos resíduos
leveneTest(Tamanho ~ Sexo, data = exercicio_1)
#> Levene's Test for Homogeneity of Variance (center = median)
#> Df F value Pr(>F)
#> group 1 2.0072 0.1676
#> 28
## Análise Teste T
t.test(Tamanho ~ Sexo, data = exercicio_1, var.equal = TRUE)
#>
#> Two Sample t-test
#>
#> data: Tamanho by Sexo
#> t = 2.2756, df = 28, p-value = 0.03072
#> alternative hypothesis: true difference in means between group f and group m is not equal to 0
#> 95 percent confidence interval:
#> 0.2356113 4.4843887
#> sample estimates:
#> mean in group f mean in group m
#> 10.08 7.72
## Gráfico
ggplot(data = exercicio_1, aes(x = Sexo, y = Tamanho)) +
geom_boxplot(width = .5, show.legend = FALSE) +
theme_bw(base_size = 14) +
geom_jitter(size = 4, width = 0.1) +
scale_x_discrete(labels=c("Fêmeas","Machos")) +
labs(title = "Dimorfismo sexual", x = "Sexo", y = "Tamanho (mm)")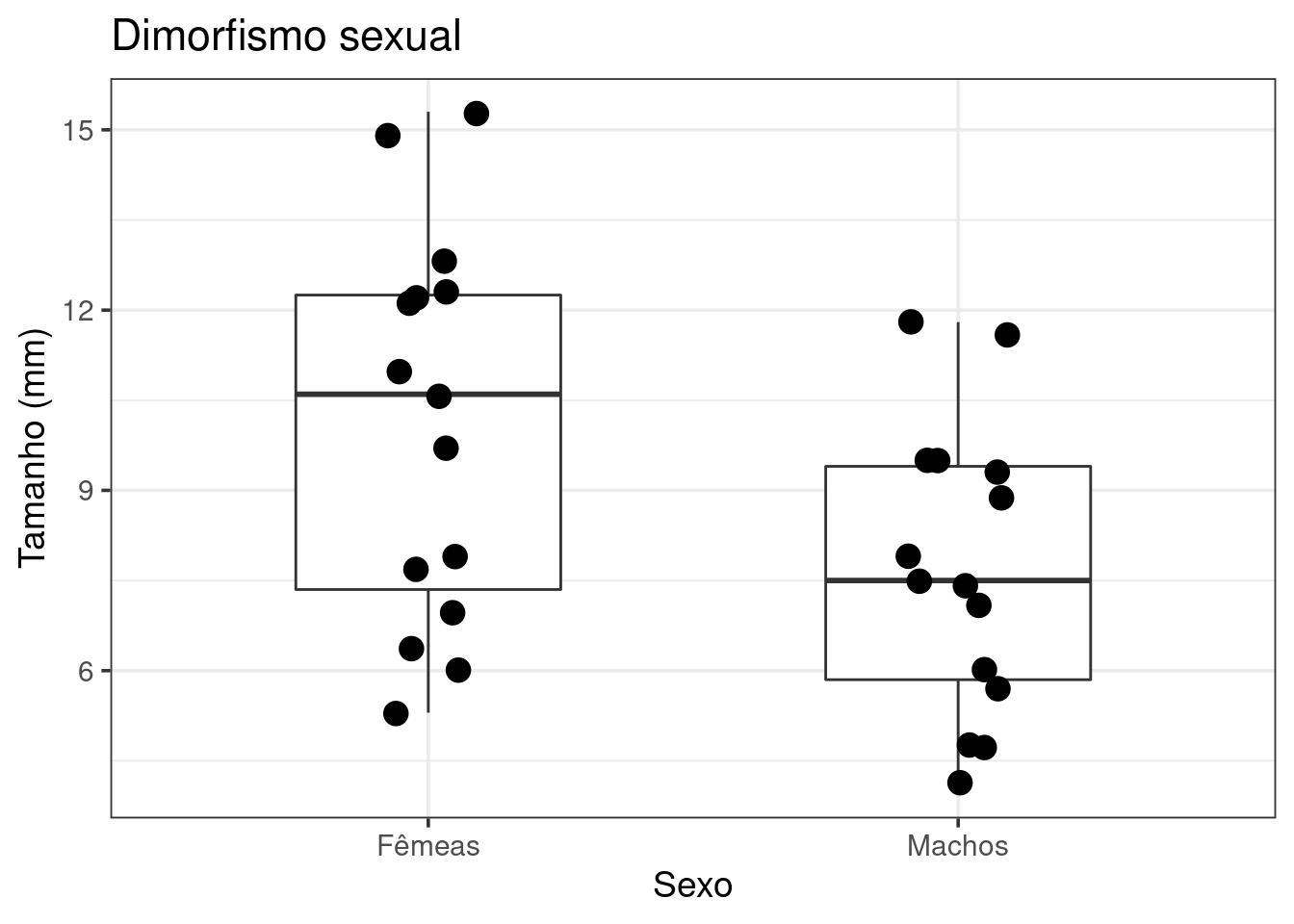
7.2 Avalie se o número de polinizadores visitando uma determinada espécie de planta é dependente da presença ou ausência de predadores. A mesma planta, em tempos diferentes, foi utilizada como unidade amostral para os tratamentos com e sem predadores. Qual a sua interpretação sobre os resultados? Faça um gráfico boxplot ligando os resultados da mesma planta com e sem a presença do predador.Use os dados Cap7_exercicio2 disponível no pacote ecodados.
Solução:
# Carregar a planilha com os dados
exercicio_2 <- ecodados::Cap7_exercicio2
## Análise Teste T Pareado
t.test(Polinizadores ~ Predadores, paired = TRUE, data = exercicio_2)
#>
#> Paired t-test
#>
#> data: Polinizadores by Predadores
#> t = 2.843, df = 19, p-value = 0.0104
#> alternative hypothesis: true difference in means is not equal to 0
#> 95 percent confidence interval:
#> 0.4088952 2.6911048
#> sample estimates:
#> mean of the differences
#> 1.55
## Gráfico
ggpaired(exercicio_2, x = "Predadores", y = "Polinizadores",
color = "Predadores", line.color = "gray", line.size = 0.8,
palette = c("darkorange", "cyan4"), width = 0.5,
point.size = 4, xlab = "Predadores",
ylab = "Número de polinizadores visitando a planta",
legend = "none") 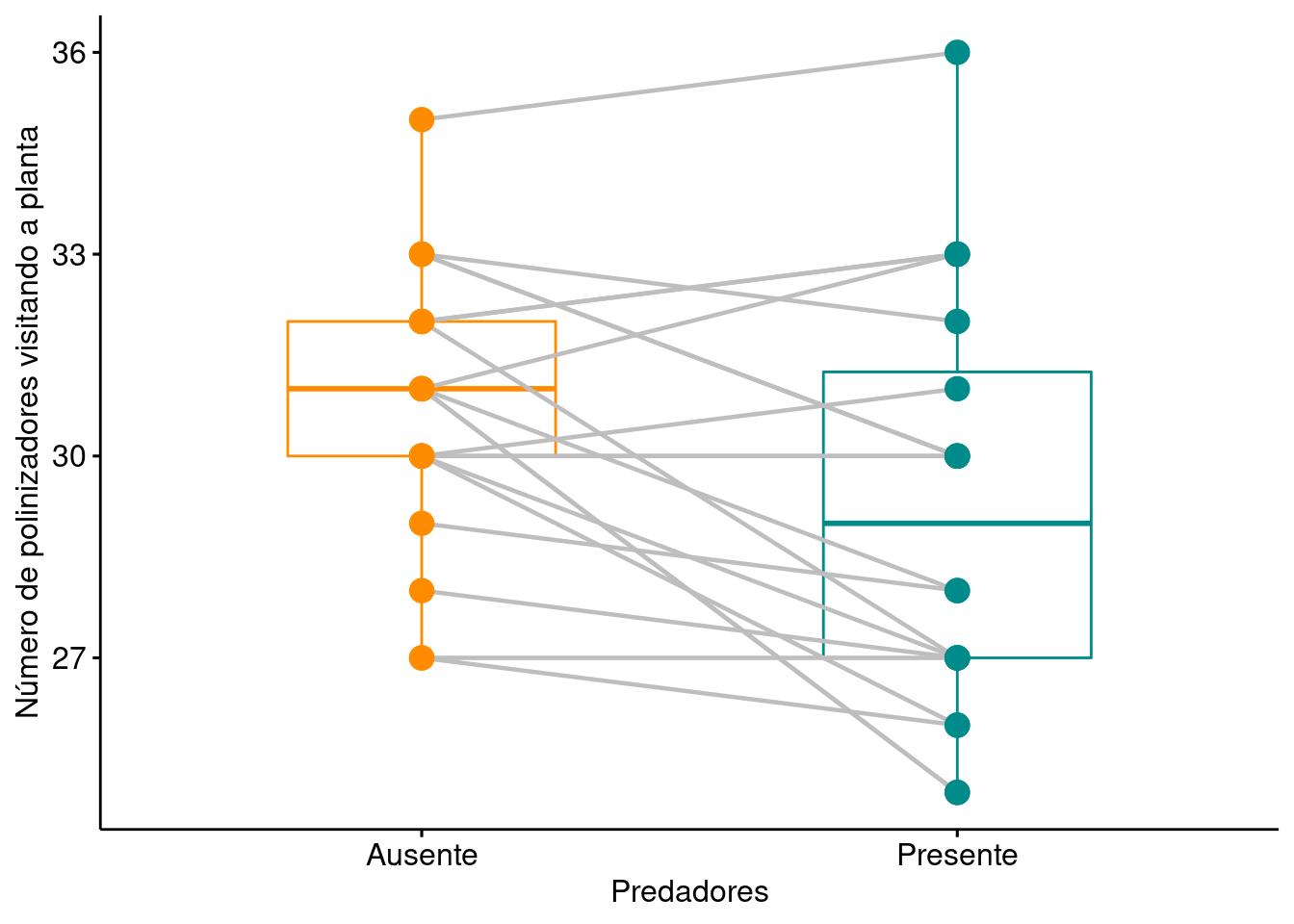
7.3 Avalie se existe correlação entre o número de filhotes nos ninhos de uma espécie de ave com o tamanho do fragmento florestal. Qual a sua interpretação dos resultados? Faça um gráfico mostrando a relação entre as variáveis. Use os dados Cap7_exercicio3 disponível no pacote ecodados.
Solução:
# Carregar a planilha com os dados
exercicio_3 <- ecodados::Cap7_exercicio3
## Análise correlação de Pearson
cor.test(~ Filhotes + Fragmentos, data = exercicio_3, method = "pearson")
#>
#> Pearson's product-moment correlation
#>
#> data: Filhotes and Fragmentos
#> t = -0.65396, df = 33, p-value = 0.5177
#> alternative hypothesis: true correlation is not equal to 0
#> 95 percent confidence interval:
#> -0.4301428 0.2287595
#> sample estimates:
#> cor
#> -0.1131098
## Gráfico
ggplot(data = exercicio_3, aes(x = Fragmentos, y = Filhotes)) +
labs(x = "Tamanho dos fragmentos (ha)", y = "Número de filhotes") +
geom_point(size = 6, shape = 21, fill = "darkorange", alpha = 0.7) +
theme(legend.position = "none") +
theme_bw(base_size = 16)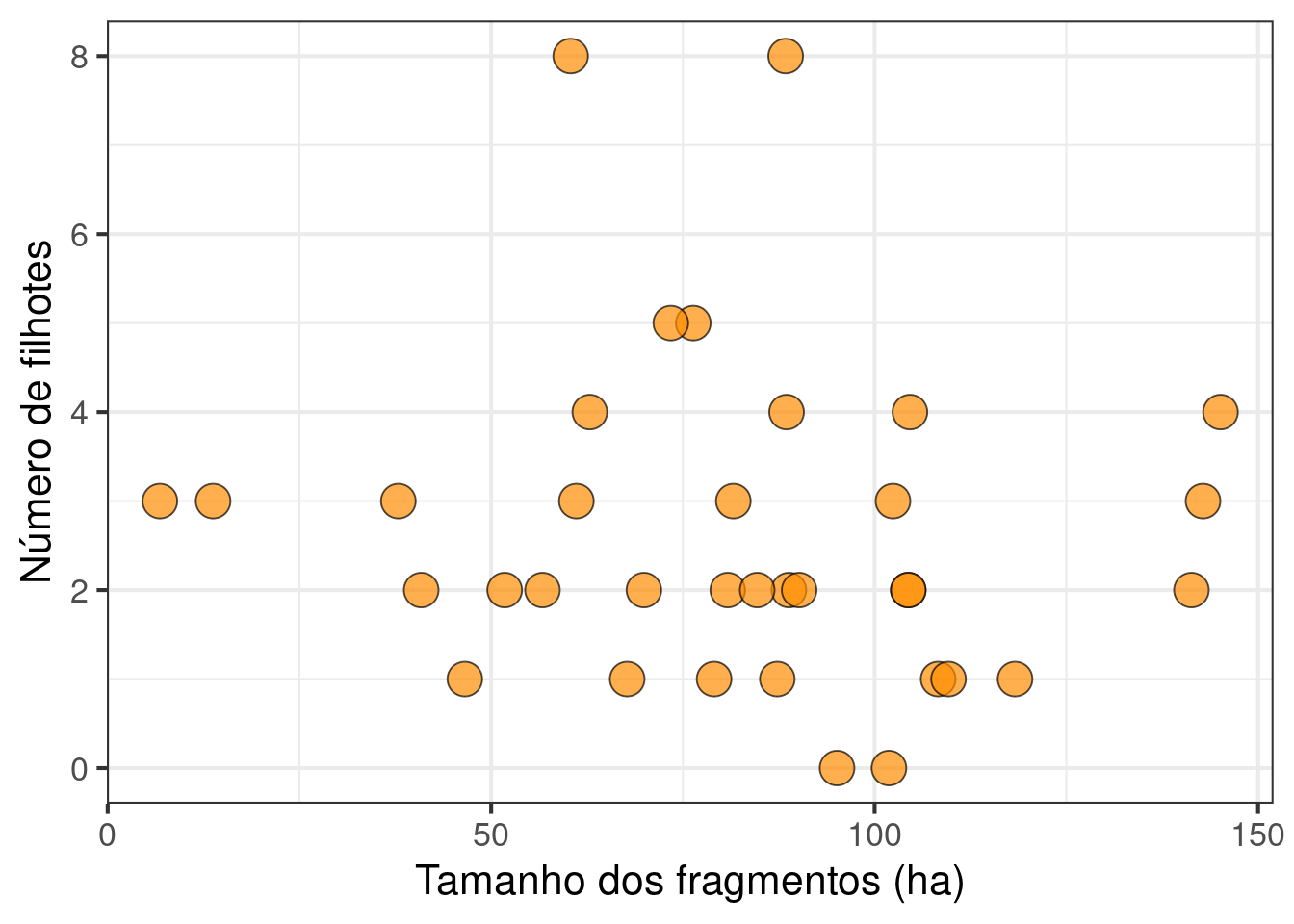
7.4 Avalie se a relação entre o tamanho da área de diferentes ilhas e a riqueza de espécies de lagartos. Qual a sua interpretação dos resultados? Faça um gráfico mostrando a relação predita pelo modelo.Use os dados Cap7_exercicio4 disponível no pacote ecodados.
Solução:
# Carregar a planilha com os dados
exercicio_4 <- ecodados::Cap7_exercicio4
## Análise Regressão Simples
modelo_regressao <- lm(Riqueza ~ Area_ilhas, data = exercicio_4)
## Análise das premissas
plot_grid(plot_model(modelo_regressao , type = "diag"))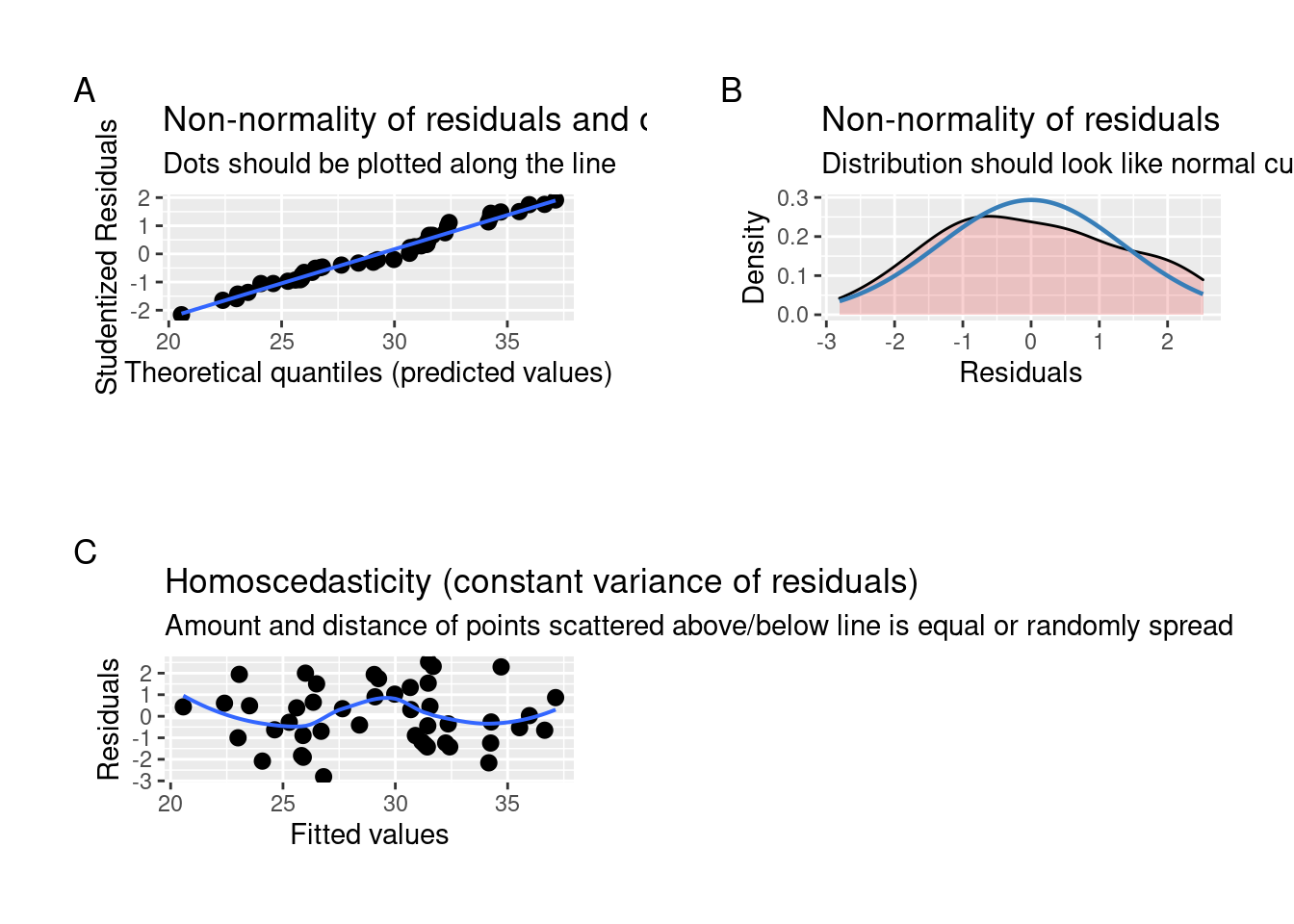
## Olhar os resultados
summary(modelo_regressao)
#>
#> Call:
#> lm(formula = Riqueza ~ Area_ilhas, data = exercicio_4)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -2.8077 -0.9996 -0.2656 0.9026 2.5195
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 3.8398 1.2816 2.996 0.00453 **
#> Area_ilhas 0.2879 0.0143 20.133 < 2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.375 on 43 degrees of freedom
#> Multiple R-squared: 0.9041, Adjusted R-squared: 0.9019
#> F-statistic: 405.3 on 1 and 43 DF, p-value: < 2.2e-16
## Gráfico
ggplot(data = exercicio_4, aes(x = Area_ilhas, y = Riqueza)) +
labs(x = "Tamanho das ilhas (km2)", y = "Riqueza de espécies de lagartos") +
geom_point(size = 6, shape = 21, fill = "darkorange", alpha = 0.7) +
theme(legend.position = "none") +
geom_smooth(method = lm, se = TRUE, color = "black") +
theme_bw(base_size = 16)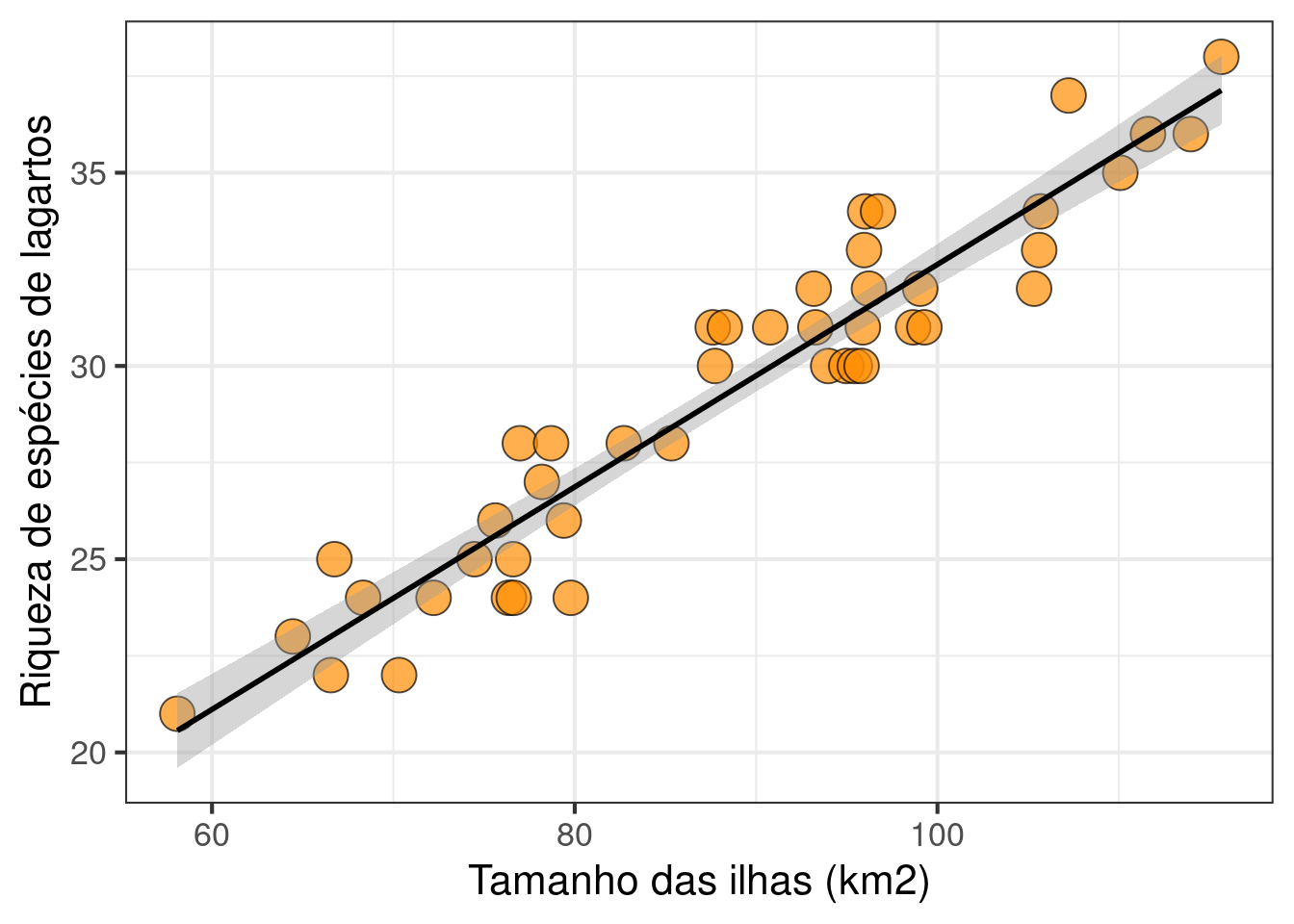
7.5 Avalie se existe relação entre a abundância de uma espécie de roedor com o tamanho da área dos fragmentos florestais e/ou a altitude. Faça uma regressão múltipla. Em seguida, crie diferentes modelos e selecione o mais parcimonioso com base no valores do teste de Likelihood-ratio test (LRT) e AIC. Qual a sua interpretação? Use os dados Cap7_exercicio5 disponível no pacote ecodados.
Solução:
# Carregar a planilha com os dados
exercicio_5 <- ecodados::Cap7_exercicio5
## Análise Regressão Múltipla
modelo_regressao_mult <- lm(Abundancia ~ Area_fragmento*Altitude, data = exercicio_5)
## Multicolinearidae
vif(modelo_regressao_mult)
#> Area_fragmento Altitude
#> 5.403688 1.786589
#> Area_fragmento:Altitude
#> 6.890149
## Análise das premissas
plot_grid(plot_model(modelo_regressao , type = "diag"))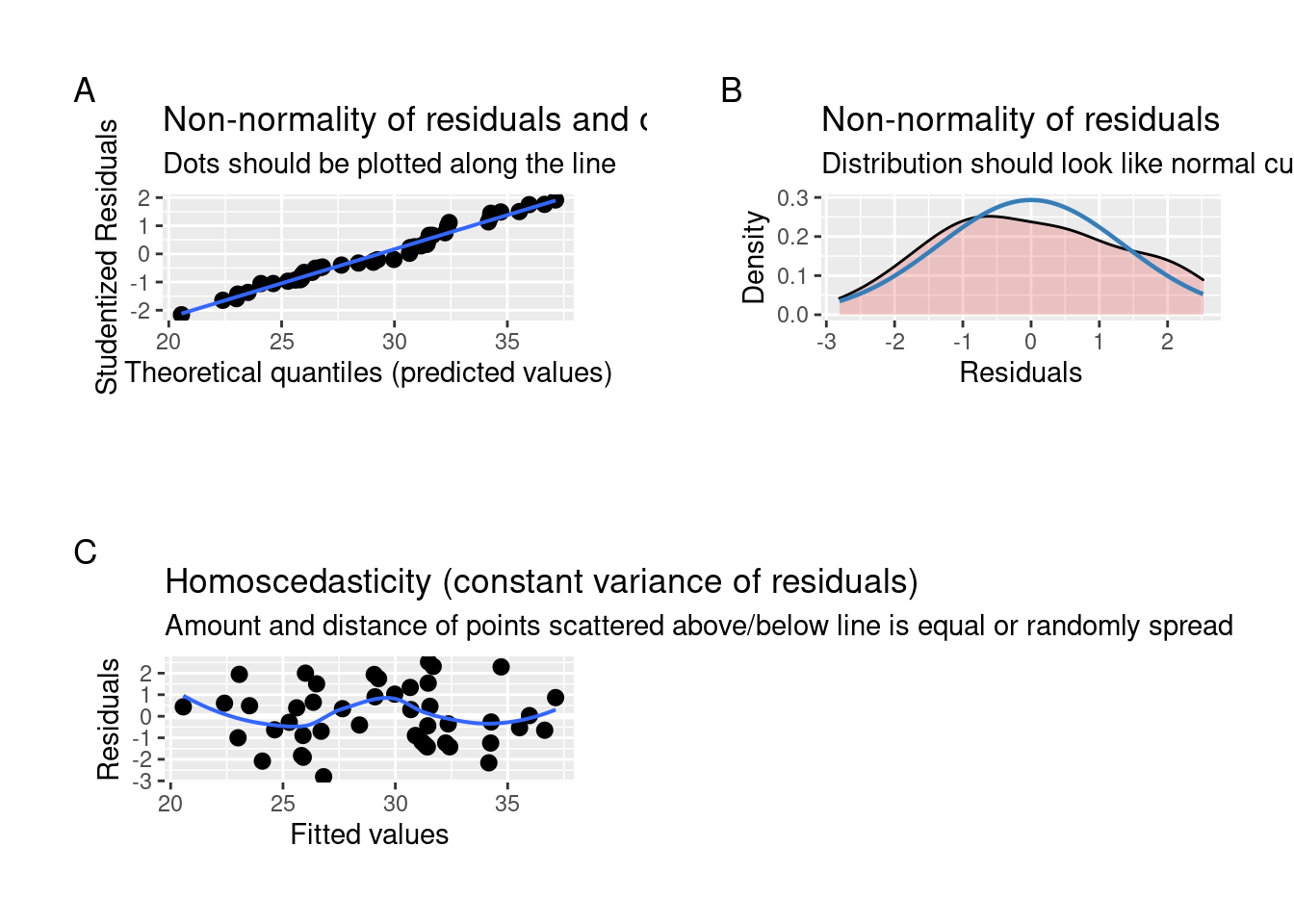
## Olhar os resultados
summary(modelo_regressao_mult)
#>
#> Call:
#> lm(formula = Abundancia ~ Area_fragmento * Altitude, data = exercicio_5)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -10.4180 -1.3524 -0.2711 1.1783 12.5283
#>
#> Coefficients:
#> Estimate Std. Error t value
#> (Intercept) 5.747e+01 8.549e-01 67.230
#> Area_fragmento -3.337e-03 3.245e-03 -1.028
#> Altitude -5.451e-03 4.859e-04 -11.218
#> Area_fragmento:Altitude 1.344e-06 1.471e-06 0.914
#> Pr(>|t|)
#> (Intercept) < 2e-16 ***
#> Area_fragmento 0.308
#> Altitude 1.69e-15 ***
#> Area_fragmento:Altitude 0.365
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 2.99 on 52 degrees of freedom
#> Multiple R-squared: 0.7986, Adjusted R-squared: 0.787
#> F-statistic: 68.73 on 3 and 52 DF, p-value: < 2.2e-16
## Vamos retirar a interação
modelo_regressao_mult_sem_interacao <- lm(Abundancia ~ Area_fragmento + Altitude, data = exercicio_5)
## Likelihood-ratio test (LRT)
lrtest(modelo_regressao_mult, modelo_regressao_mult_sem_interacao)
#> Likelihood ratio test
#>
#> Model 1: Abundancia ~ Area_fragmento * Altitude
#> Model 2: Abundancia ~ Area_fragmento + Altitude
#> #Df LogLik Df Chisq Pr(>Chisq)
#> 1 5 -138.71
#> 2 4 -139.16 -1 0.8917 0.345
## Vamos verificar o modelo só com a altitude
modelo_regressao_mult_sem_fragmento <- lm(Abundancia ~ Altitude, data = exercicio_5)
lrtest(modelo_regressao_mult_sem_interacao, modelo_regressao_mult_sem_fragmento)
#> Likelihood ratio test
#>
#> Model 1: Abundancia ~ Area_fragmento + Altitude
#> Model 2: Abundancia ~ Altitude
#> #Df LogLik Df Chisq Pr(>Chisq)
#> 1 4 -139.16
#> 2 3 -139.28 -1 0.2364 0.6268
## Vamos verificar o modelo só com o intercepto
modelo_regressao_mult_nulo <- lm(Abundancia ~ 1, data = exercicio_5)
lrtest(modelo_regressao_mult_sem_fragmento, modelo_regressao_mult_nulo)
#> Likelihood ratio test
#>
#> Model 1: Abundancia ~ Altitude
#> Model 2: Abundancia ~ 1
#> #Df LogLik Df Chisq Pr(>Chisq)
#> 1 3 -139.28
#> 2 2 -183.58 -1 88.611 < 2.2e-16 ***
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Outra alternativa é usar o AIC para seleção dos modelos
## modelo só com a área do fragmento
modelo_regressao_mult_sem_altitude <- lm(Abundancia ~ Area_fragmento, data = exercicio_5)
AICc <- ICtab(modelo_regressao_mult, modelo_regressao_mult_sem_interacao,
modelo_regressao_mult_sem_fragmento,modelo_regressao_mult_nulo,
modelo_regressao_mult_sem_altitude,
type = c("AIC"), weights = TRUE,
delta = TRUE, sort = TRUE)
AICc
#> dAIC df weight
#> modelo_regressao_mult_sem_fragmento 0.0 3 0.61
#> modelo_regressao_mult_sem_interacao 1.8 4 0.25
#> modelo_regressao_mult 2.9 5 0.14
#> modelo_regressao_mult_sem_altitude 85.6 3 <0.001
#> modelo_regressao_mult_nulo 86.6 2 <0.001
## Gráfico
ggplot(data = exercicio_5, aes(x = Altitude, y = Abundancia)) +
labs(x = "Altitude (m)", y = "Abundância da espécie") +
geom_point(size = 6, shape = 21, fill = "darkorange", alpha = 0.7) +
theme(legend.position = "none") +
geom_smooth(method = lm, se = TRUE, color = "black") +
theme_bw(base_size = 16)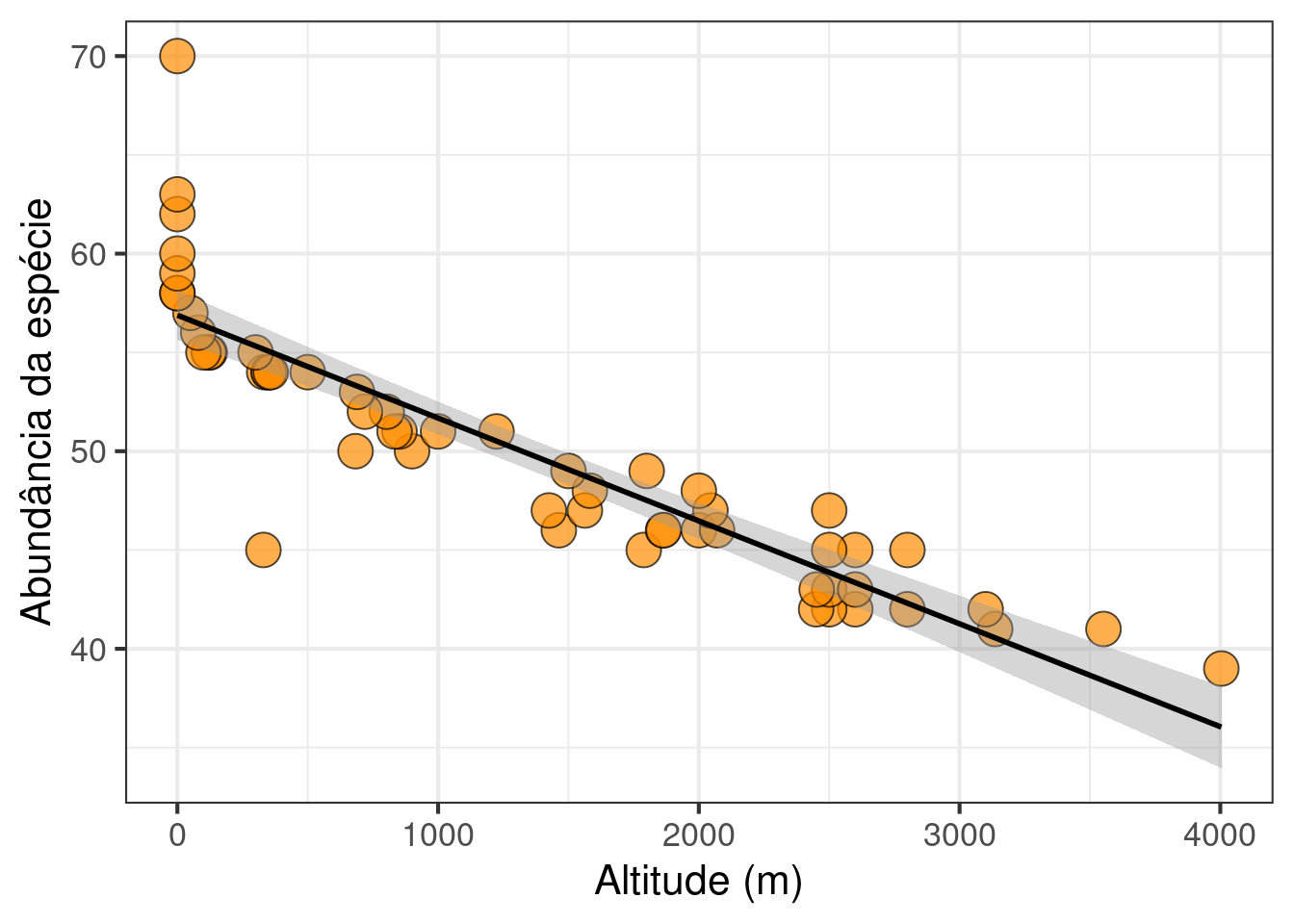
7.6 Avalie se o local que machos territoriais ocupam (pasto, cana, floresta) influência no peso dos indivíduos. Qual a sua interpretação dos resultados? Faça um gráfico com os resultados. Use os dados Cap7_exercicio6 disponível no pacote ecodados.
Solução:
# Carregar a planilha com os dados
exercicio_6 <- ecodados::Cap7_exercicio6
## Análise anova um fator
modelo_aov <- aov(Peso ~ Local, data = exercicio_6)
## Normalidade
shapiro.test(residuals(modelo_aov))
#>
#> Shapiro-Wilk normality test
#>
#> data: residuals(modelo_aov)
#> W = 0.95361, p-value = 0.211
## Homogeneidade da variância
bartlett.test(Peso ~ Local, data = exercicio_6)
#>
#> Bartlett test of homogeneity of variances
#>
#> data: Peso by Local
#> Bartlett's K-squared = 0.06087, df = 2, p-value =
#> 0.97
## Olhar os resultados
anova(modelo_aov)
#> Analysis of Variance Table
#>
#> Response: Peso
#> Df Sum Sq Mean Sq F value Pr(>F)
#> Local 2 20.0536 10.0268 248.47 < 2.2e-16 ***
#> Residuals 27 1.0896 0.0404
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Diferenças entre os tratamentos
TukeyHSD(modelo_aov)
#> Tukey multiple comparisons of means
#> 95% family-wise confidence level
#>
#> Fit: aov(formula = Peso ~ Local, data = exercicio_6)
#>
#> $Local
#> diff lwr upr p adj
#> Floresta-Cana 1.1125 0.8897525 1.3352475 0
#> Pastagem-Cana -0.8859 -1.1086475 -0.6631525 0
#> Pastagem-Floresta -1.9984 -2.2211475 -1.7756525 0
## Gráfico
ggplot(data = exercicio_6,
aes(x = Local, y = Peso)) +
geom_boxplot(width = .5, show.legend = FALSE) +
geom_jitter(size = 4, width = 0.1) +
geom_text(x = 1, y = 17.5, label = "a", color = "black", size = 5) +
geom_text(x = 2, y = 18.5, label = "b", color = "black", size = 5) +
geom_text(x = 3, y = 16.5, label = "c", color = "black", size = 5) +
ylim(16, 18.5) +
theme_bw(base_size = 16) +
labs(x = "Local", y = "Peso (g)")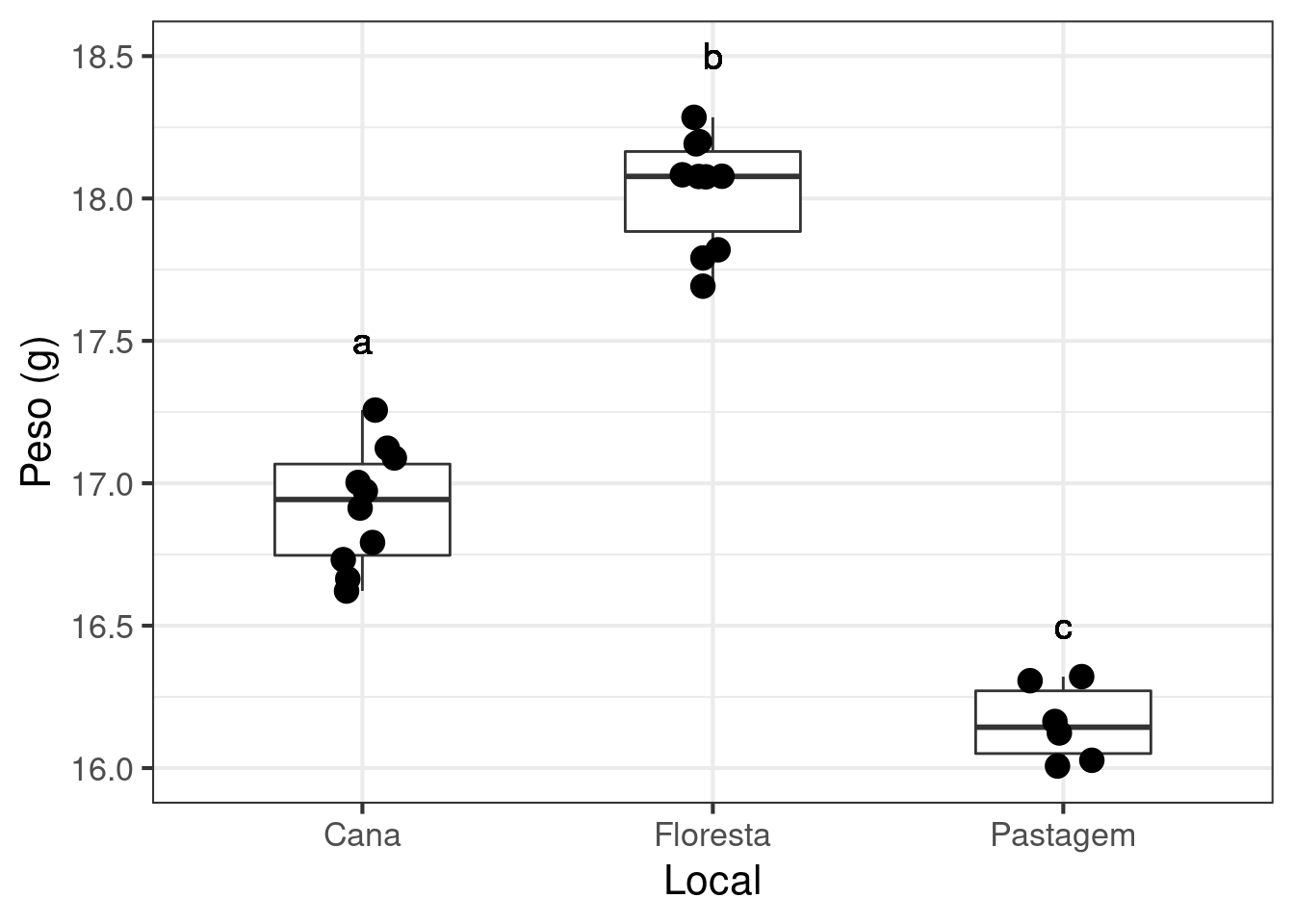
7.7 Avalie se a abundância de formigas está relacionada com o fato das domácias estarem abertas ou fechadas e com a idade das domácias. Verifique a interação entre os fatores. Qual a sua interpretação dos resultados? Faça um gráfico com os resultados. Use os dados Cap7_exercicio7 disponível no pacote ecodados.
Solução:
# Carregar a planilha com os dados
exercicio_7 <- ecodados::Cap7_exercicio7
## Análise anova dois fatores
modelo_aov_2 <- aov(Abundancia ~ Domacea * Idade, data = exercicio_7)
## Olhar os resultados
anova(modelo_aov_2)
#> Analysis of Variance Table
#>
#> Response: Abundancia
#> Df Sum Sq Mean Sq F value Pr(>F)
#> Domacea 1 931.22 931.22 32.993 1.528e-06 ***
#> Idade 1 555.02 555.02 19.664 8.334e-05 ***
#> Domacea:Idade 1 455.63 455.63 16.143 0.0002862 ***
#> Residuals 36 1016.10 28.22
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Gráfico
ggplot(data = exercicio_7,
aes(y = Abundancia, x = Domacea, color = Idade)) +
geom_boxplot() +
stat_summary(fun = mean, geom ="point", aes(group = Idade, x = Domacea),
color = "black", position = position_dodge(0.7), size = 4) +
geom_link(aes(x = 0.85, y = 27, xend = 1.8, yend = 24), color = "darkorange",
lwd = 1.3, linetype = 2) +
geom_link(aes(x = 1.17, y = 26.5, xend = 2.15, yend = 10), color = "cyan4",
lwd = 1.3, linetype = 2) +
labs(x = "Condição da domácea",
y = "Abundância de formigas") +
theme_bw(base_size = 16)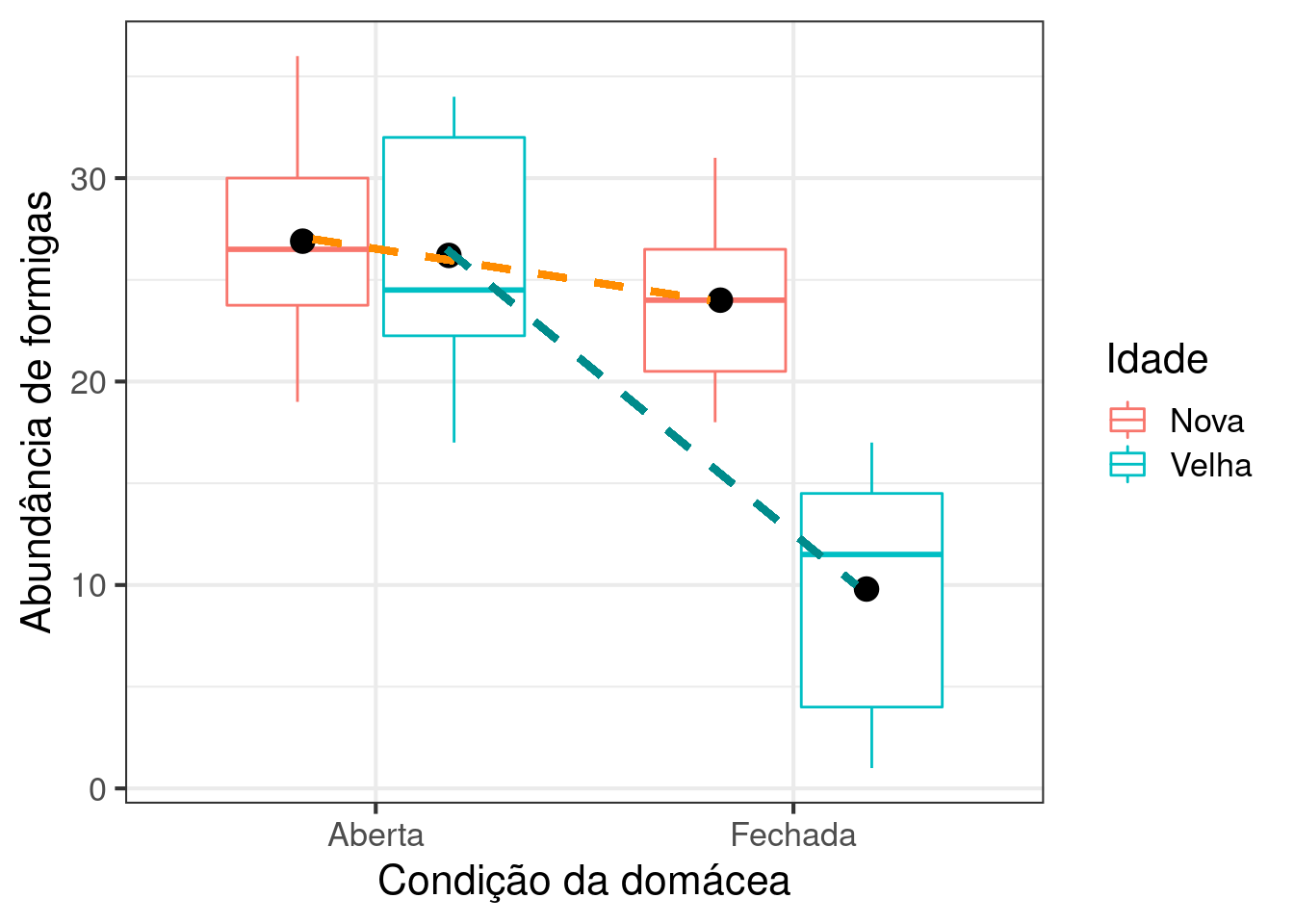
7.8 Avalie se o número de parasitas está relacionado com o tamanho corporal de fêmeas de uma espécie de ave. Além disso, use a idade das aves como uma co-variável explicando o número de parasitas. Qual a sua interpretação dos resultados? Faça um gráfico com os resultados. Use os dados Cap7_exercicio8 disponível no pacote ecodados.
Solução:
# Carregar a planilha com os dados
exercicio_8 <- ecodados::Cap7_exercicio8
## Análise ancova
modelo_ancova <- lm(Parasitas ~ Femeas * Idade, data = exercicio_8)
## Verificar as premissas
plot_grid(plot_model(modelo_ancova, type = "diag"))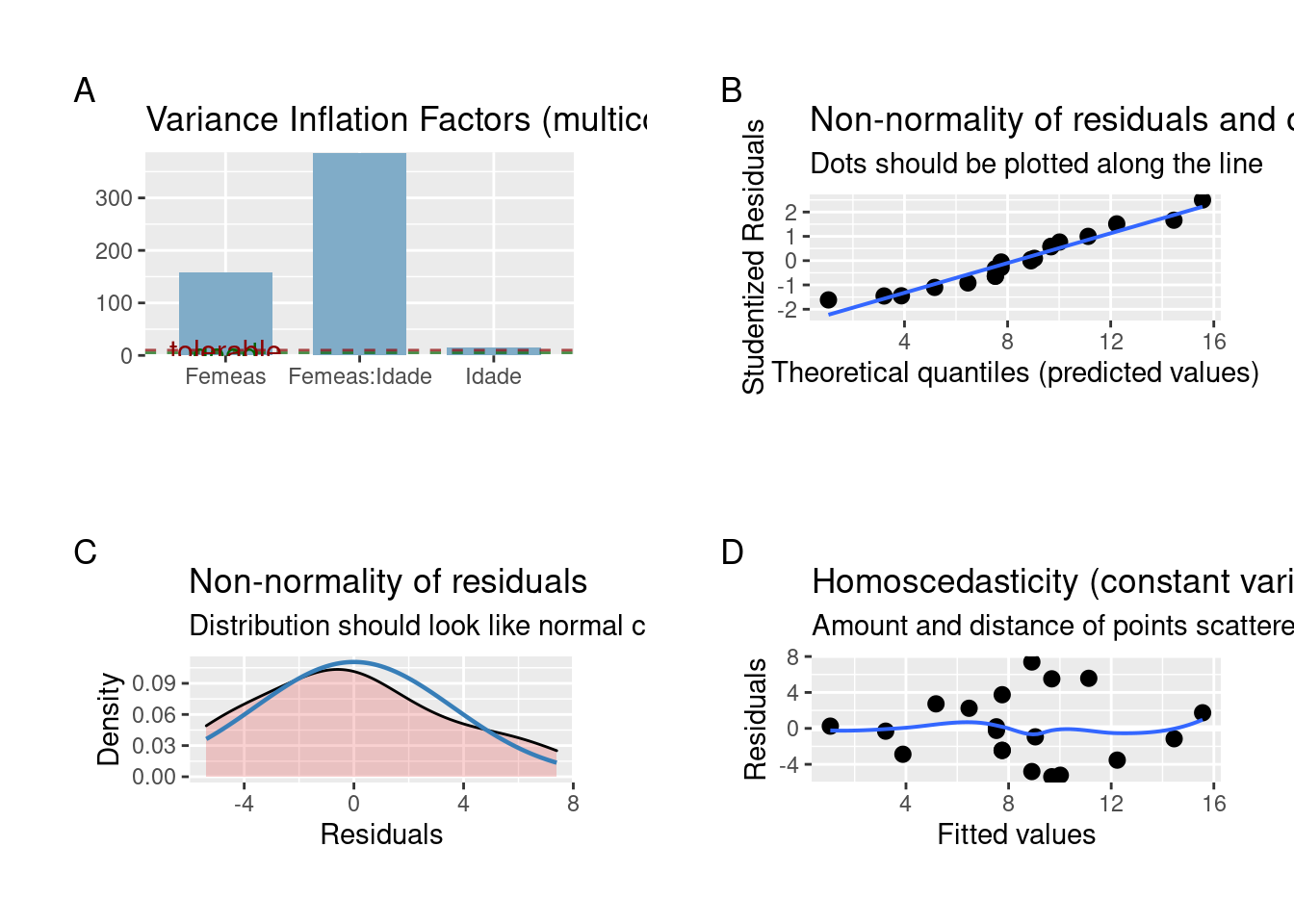
## Olhar os resultados
anova(modelo_ancova)
#> Analysis of Variance Table
#>
#> Response: Parasitas
#> Df Sum Sq Mean Sq F value Pr(>F)
#> Femeas 2 111.577 55.789 3.2153 0.06885 .
#> Idade 1 113.527 113.527 6.5431 0.02185 *
#> Femeas:Idade 2 10.866 5.433 0.3131 0.73582
#> Residuals 15 260.261 17.351
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Criando modelo sem interação
modelo_ancova2 <- lm(Parasitas ~ Femeas + Idade, data = exercicio_8)
## Likelihood-ratio test
lrtest(modelo_ancova, modelo_ancova2)
#> Likelihood ratio test
#>
#> Model 1: Parasitas ~ Femeas * Idade
#> Model 2: Parasitas ~ Femeas + Idade
#> #Df LogLik Df Chisq Pr(>Chisq)
#> 1 7 -56.228
#> 2 5 -56.657 -2 0.859 0.6508
anova(modelo_ancova2)
#> Analysis of Variance Table
#>
#> Response: Parasitas
#> Df Sum Sq Mean Sq F value Pr(>F)
#> Femeas 2 111.58 55.789 3.4980 0.05341 .
#> Idade 1 113.53 113.527 7.1183 0.01622 *
#> Residuals 17 271.13 15.949
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Criando modelo sem tamanho do corpo
modelo_ancova3 <- lm(Parasitas ~ Idade, data = exercicio_8)
## Likelihood-ratio test
lrtest(modelo_ancova2, modelo_ancova3)
#> Likelihood ratio test
#>
#> Model 1: Parasitas ~ Femeas + Idade
#> Model 2: Parasitas ~ Idade
#> #Df LogLik Df Chisq Pr(>Chisq)
#> 1 5 -56.657
#> 2 3 -57.087 -2 0.8584 0.651
anova(modelo_ancova3)
#> Analysis of Variance Table
#>
#> Response: Parasitas
#> Df Sum Sq Mean Sq F value Pr(>F)
#> Idade 1 213.79 213.792 14.382 0.001231 **
#> Residuals 19 282.44 14.865
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Gráfico
ggplot(data = exercicio_8, aes(x = Idade, y = Parasitas)) +
labs(x = "Idade das aves", y = "Número de parasitas") +
geom_point(size = 6, shape = 19, alpha = 0.7) +
theme(legend.position = "none") +
geom_smooth(method = lm, se = TRUE, color = "black") +
theme_bw(base_size = 16)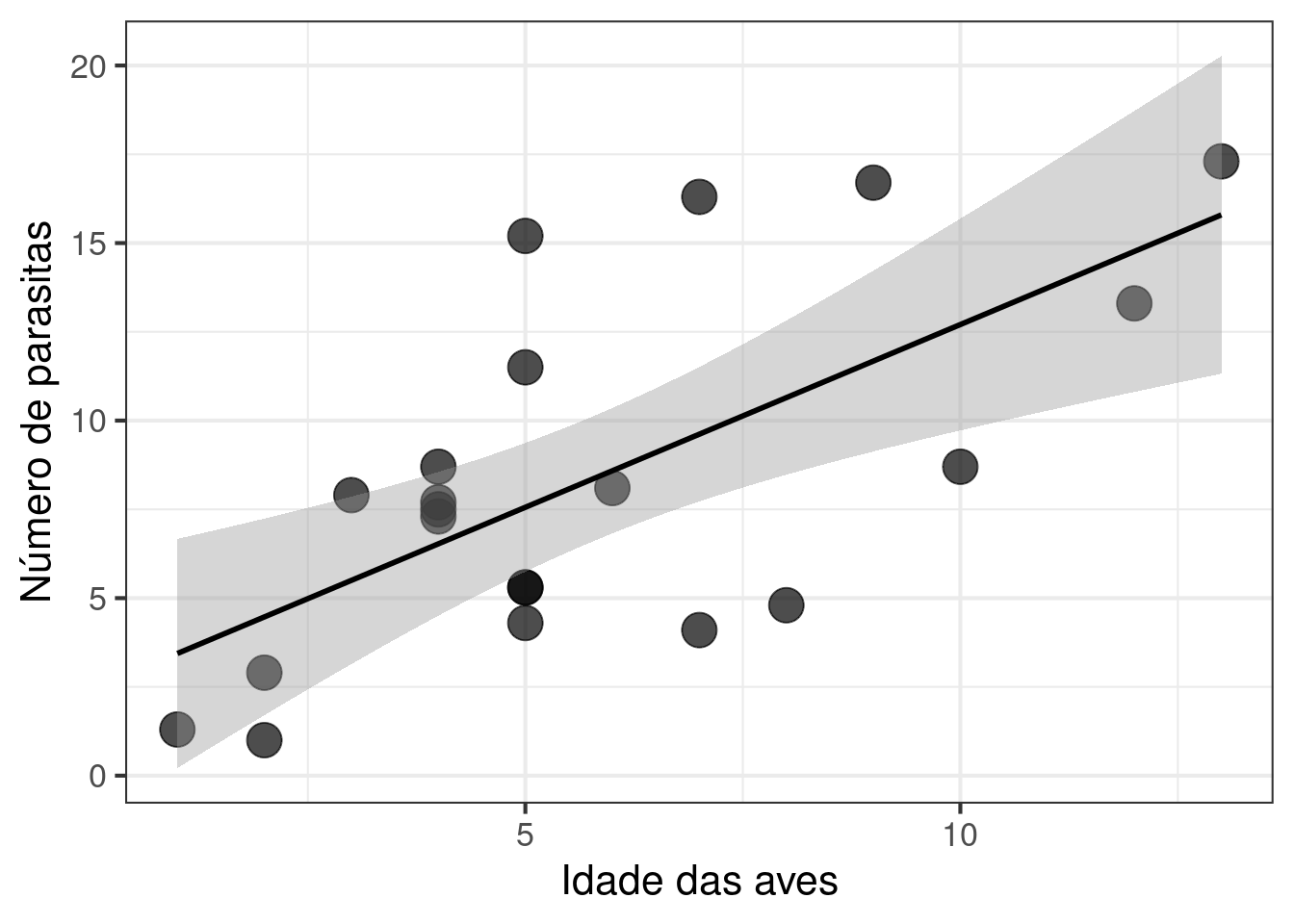
7.9 Avalie se a presença ou ausência de predadores afeta a riqueza de macroinvertebrados em 10 lagos. Os tratamentos dos predadores foram realizados nos mesmos lagos. Qual a sua interpretação dos resultados? Faça um gráfico com os resultados.Use os dados Cap7_exercicio9 disponível no pacote ecodados.
Solução:
# Carregar a planilha com os dados
exercicio_9 <- ecodados::Cap7_exercicio9
## Análise anova em blocos
model_bloco <- aov(Riqueza ~ Predadores + Error(Lago), data = exercicio_9)
summary(model_bloco)
#>
#> Error: Lago
#> Df Sum Sq Mean Sq F value Pr(>F)
#> Residuals 1 0.2561 0.2561
#>
#> Error: Within
#> Df Sum Sq Mean Sq F value Pr(>F)
#> Predadores 1 120.0 120.05 4.743 0.0438 *
#> Residuals 17 430.2 25.31
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Gráfico
ggplot(data = exercicio_9, aes(x = Predadores, y = Riqueza)) +
geom_boxplot(color = "black", show.legend = FALSE, alpha = 0.4) +
geom_jitter(size = 4, width = 0.1) +
labs(x = "Predadores", y = "Riqueza de macroinvertebrados") +
theme_bw(base_size = 16)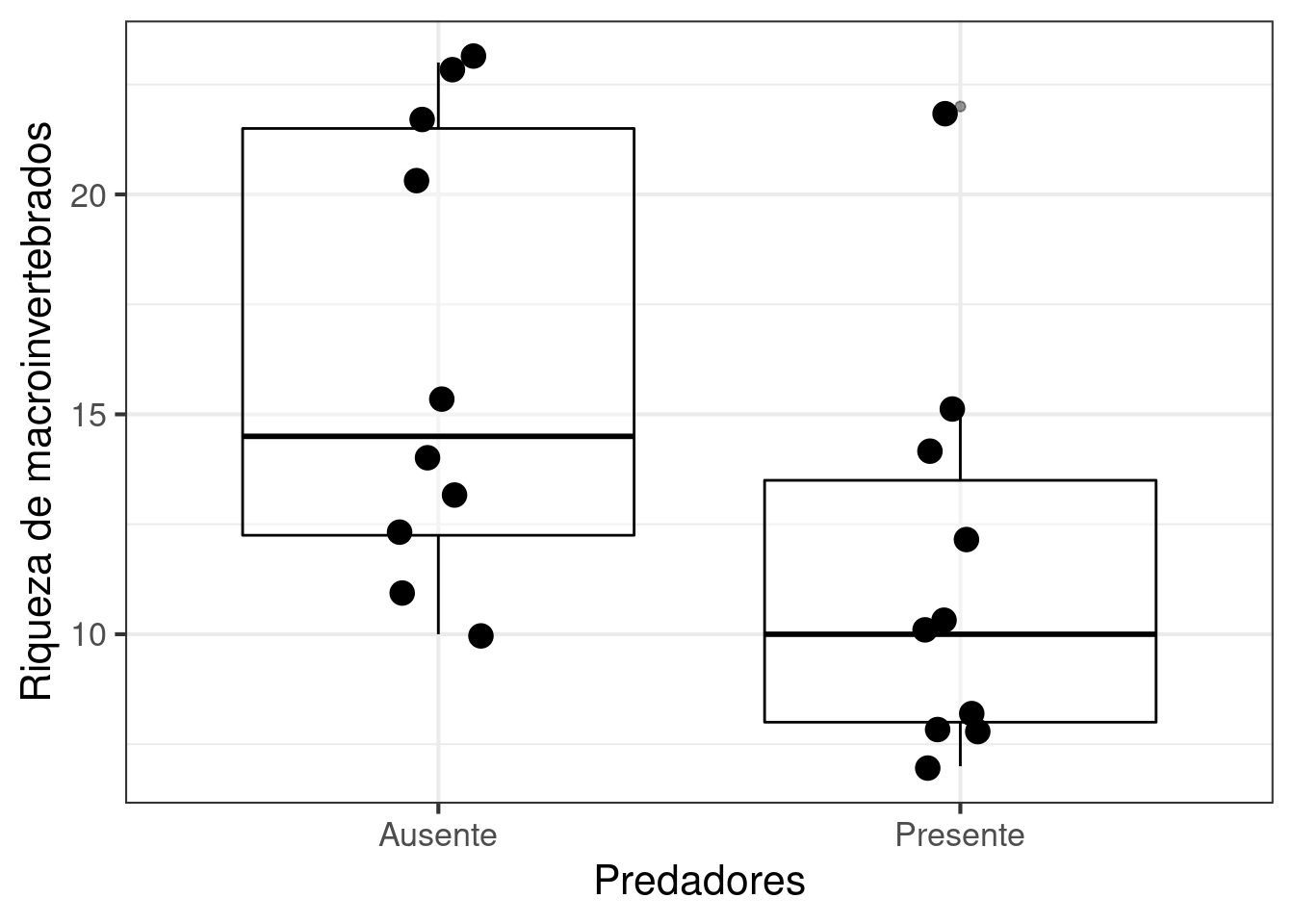
7.10 Avalie se a precipitação anual afeta a riqueza de espécies de anuros em 44 localidades na Mata Atlântica. Use as coordenadas geográficas para controlar o efeito da autocorrelação espacial. Qual a sua interpretação dos resultados das análises com e sem levar em consideração a autocorrelação espacial? Use os dados anuros_ambientais disponível no pacote ecodados.
Solução:
# Carregar a planilha com os dados
exercicio_10 <- ecodados::anuros_ambientais
## Modelo gls sem estrutura espacial
no_spat_gls <- gls(Riqueza ~ Prec_anual, exercicio_10, method = "REML")
## Covariância esférica
espher_model <- gls(Riqueza ~ Prec_anual, exercicio_10,
corSpher(form = ~Latitude + Longitude, nugget = TRUE))
## Covariância exponencial
expon_model <- gls(Riqueza ~ Prec_anual, exercicio_10,
corExp(form = ~Latitude + Longitude, nugget = TRUE))
## Covariância Gaussiana
gauss_model <- gls(Riqueza ~ Prec_anual, exercicio_10,
corGaus(form = ~Latitude + Longitude, nugget = TRUE))
## Covariância linear
cor_linear_model <- gls(Riqueza ~ Prec_anual, exercicio_10,
corLin(form = ~Latitude + Longitude, nugget = TRUE))
## Covariância razão quadrática
ratio_model <- gls(Riqueza ~ Prec_anual, exercicio_10,
corRatio(form = ~Latitude + Longitude, nugget = TRUE))
## Seleção de modelos
aic_fit <- AIC(no_spat_gls, espher_model, expon_model,
cor_linear_model, gauss_model,ratio_model)
aic_fit %>% arrange(AIC)
#> df AIC
#> cor_linear_model 5 344.1434
#> gauss_model 5 344.3118
#> ratio_model 5 344.8400
#> no_spat_gls 3 345.4316
#> espher_model 5 345.6006
#> expon_model 5 346.2936
## Gráfico
plot(residuals(cor_linear_model, type = "normalized") ~ fitted(cor_linear_model))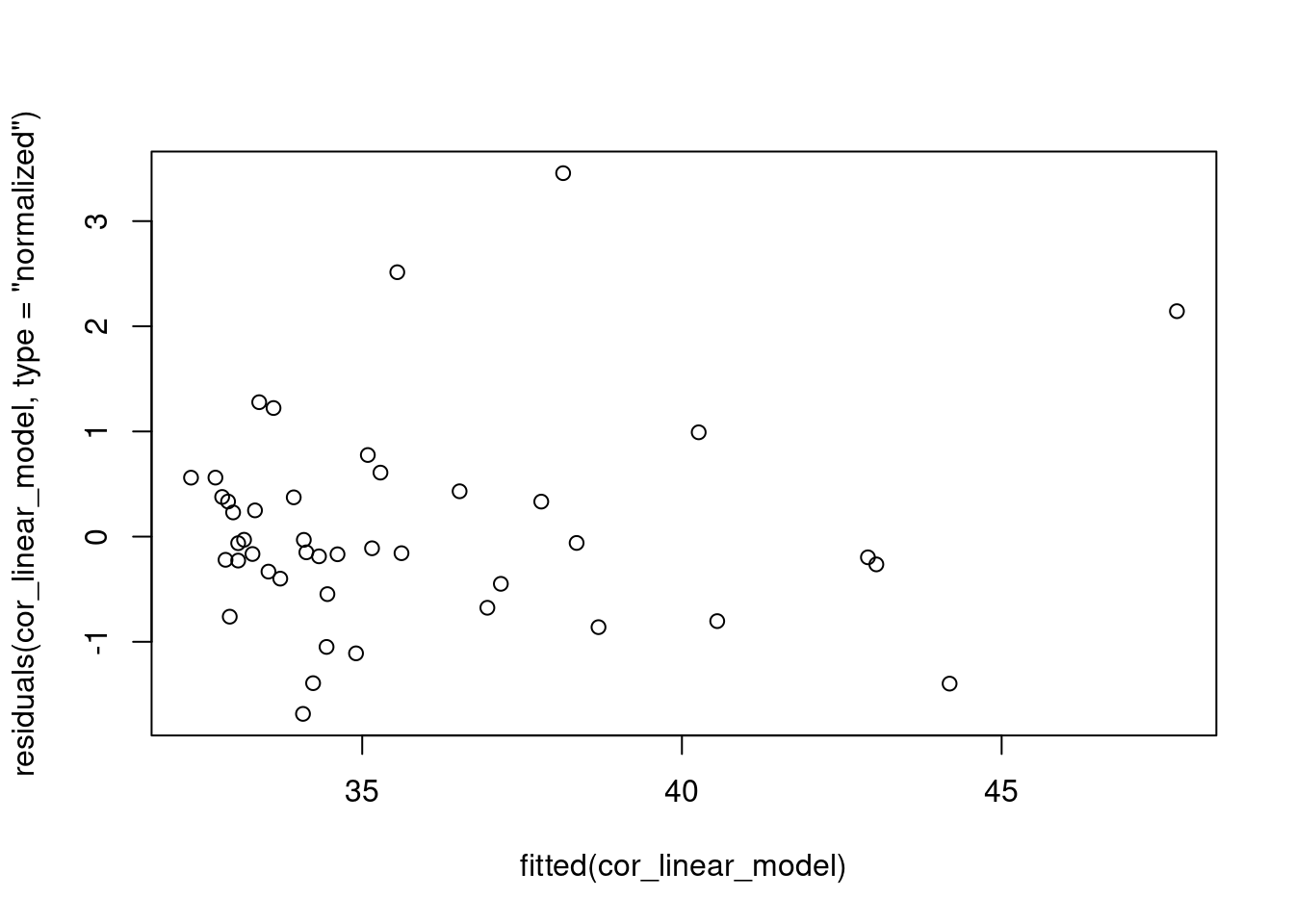
## Varigrama
cor_linear_variog <- Variogram(cor_linear_model, form = ~Latitude + Longitude,
resType = "normalized")
plot(cor_linear_variog, main = "Variograma como Modelo de Covariância Linear")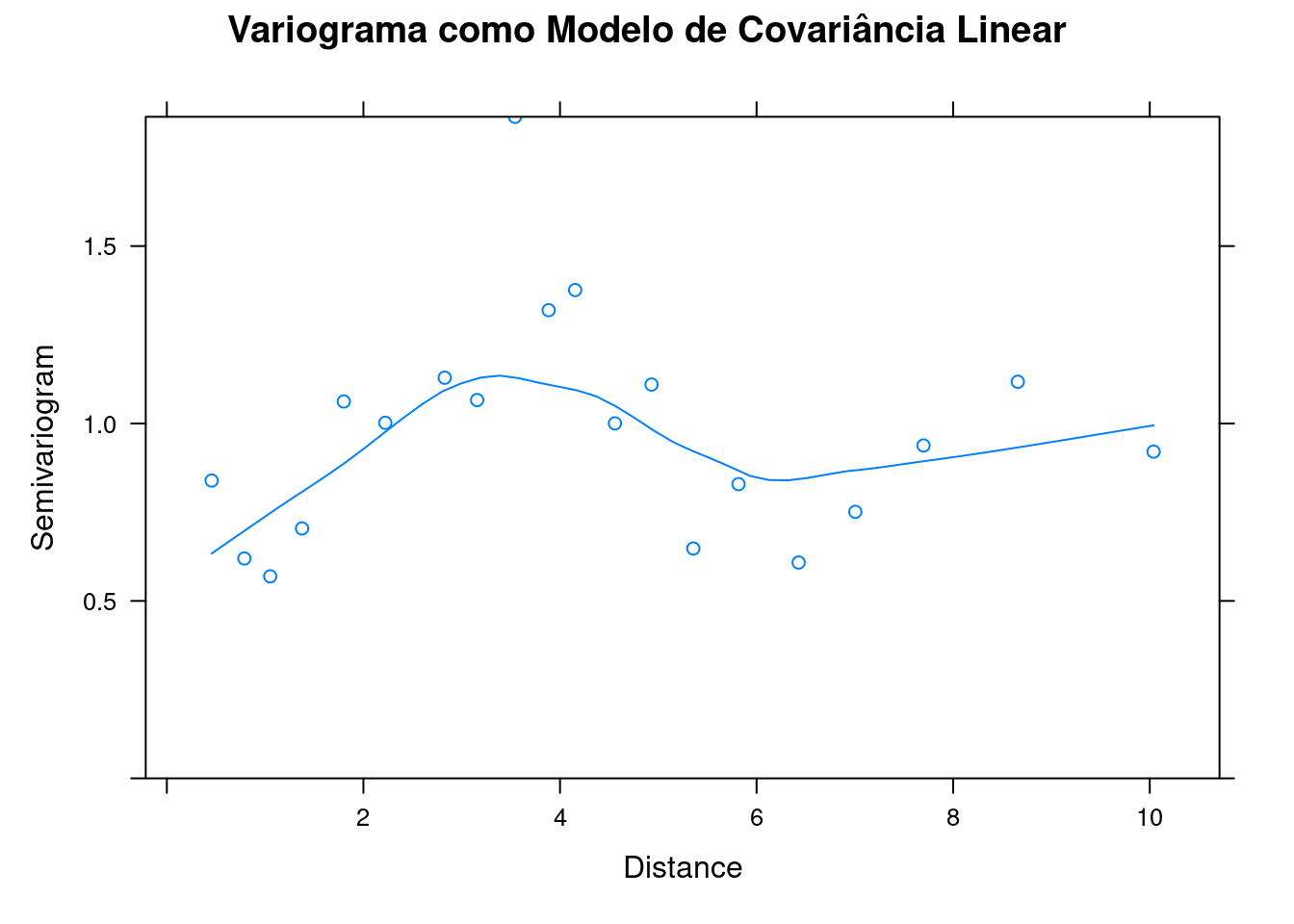
## Resumo dos modelos
summary(cor_linear_model)$tTable
#> Value Std.Error t-value p-value
#> (Intercept) 17.25918513 73.686338088 0.234225 0.8159483
#> Prec_anual 0.01316726 0.008113421 1.622899 0.1120944
summary(no_spat_gls)$tTable
#> Value Std.Error t-value p-value
#> (Intercept) -3.35797556 8.99912469 -0.3731447 0.7109175029
#> Prec_anual 0.02288015 0.00630715 3.6276526 0.0007686691