Cap. 8 - Modelos Lineares Generalizados
# Pacotes necessários
library(tidyverse)
library(ordinal)
library(naniar)
library(generalhoslem)
library(ecolottery)
library(DHARMa)
library(parameters)
library(piecewiseSEM)
library(vcd)
library(effectsize)8.1 Baixe estes dados que foram coletados numa pesquisa de opinião sobre uso de vídeo games por 91 estudantes de graduação no outono de 1994. Utilizando estes dados, constra um modelo: 1) Predizer a frequência com que uma pessoa joga vídeo game em função da idade; 2) Predizer a nota do estudante em função do tempo que jogou na semana antes da entrevista. Dica: esses são dados ordinais!
Solução:
#---Importando os dados
videogame <- read.table("https://www.stat.berkeley.edu/~statlabs/data/video.data", h=TRUE, na.strings = "99")
head(videogame)
#> time like where freq busy educ sex age home math work own
#> 1 2.0 3 3 2 0 1 0 19 1 0 10 1
#> 2 0.0 3 3 3 0 0 0 18 1 1 0 1
#> 3 0.0 3 1 3 0 0 1 19 1 0 0 1
#> 4 0.5 3 3 3 0 1 0 19 1 0 0 1
#> 5 0.0 3 3 4 0 1 0 19 1 1 0 0
#> 6 0.0 3 2 4 0 0 1 19 0 0 12 0
#> cdrom email grade
#> 1 0 1 4
#> 2 1 1 2
#> 3 0 1 3
#> 4 0 1 3
#> 5 0 1 3
#> 6 0 0 3
str(videogame)
#> 'data.frame': 91 obs. of 15 variables:
#> $ time : num 2 0 0 0.5 0 0 0 0 2 0 ...
#> $ like : int 3 3 3 3 3 3 4 3 3 3 ...
#> $ where: int 3 3 1 3 3 2 3 3 2 3 ...
#> $ freq : int 2 3 3 3 4 4 4 4 1 4 ...
#> $ busy : int 0 0 0 0 0 0 0 0 1 0 ...
#> $ educ : int 1 0 0 1 1 0 0 0 1 1 ...
#> $ sex : int 0 0 1 0 0 1 1 0 1 1 ...
#> $ age : int 19 18 19 19 19 19 20 19 19 19 ...
#> $ home : int 1 1 1 1 1 0 1 1 0 1 ...
#> $ math : int 0 1 0 0 1 0 1 0 0 1 ...
#> $ work : int 10 0 0 0 0 12 10 13 0 0 ...
#> $ own : int 1 1 1 1 0 0 1 0 0 1 ...
#> $ cdrom: int 0 1 0 0 0 0 0 0 0 0 ...
#> $ email: int 1 1 1 1 1 0 1 1 0 1 ...
#> $ grade: int 4 2 3 3 3 3 3 3 4 4 ...
is.na(videogame$freq)
#> [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
#> [10] FALSE FALSE FALSE FALSE FALSE FALSE TRUE FALSE FALSE
#> [19] FALSE TRUE FALSE FALSE FALSE TRUE TRUE FALSE FALSE
#> [28] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
#> [37] FALSE FALSE FALSE FALSE TRUE FALSE FALSE FALSE TRUE
#> [46] FALSE FALSE FALSE TRUE FALSE FALSE TRUE FALSE FALSE
#> [55] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE
#> [64] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
#> [73] TRUE FALSE TRUE FALSE TRUE FALSE FALSE FALSE FALSE
#> [82] TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
#> [91] FALSE
#---Explorando os dados
vis_miss(videogame)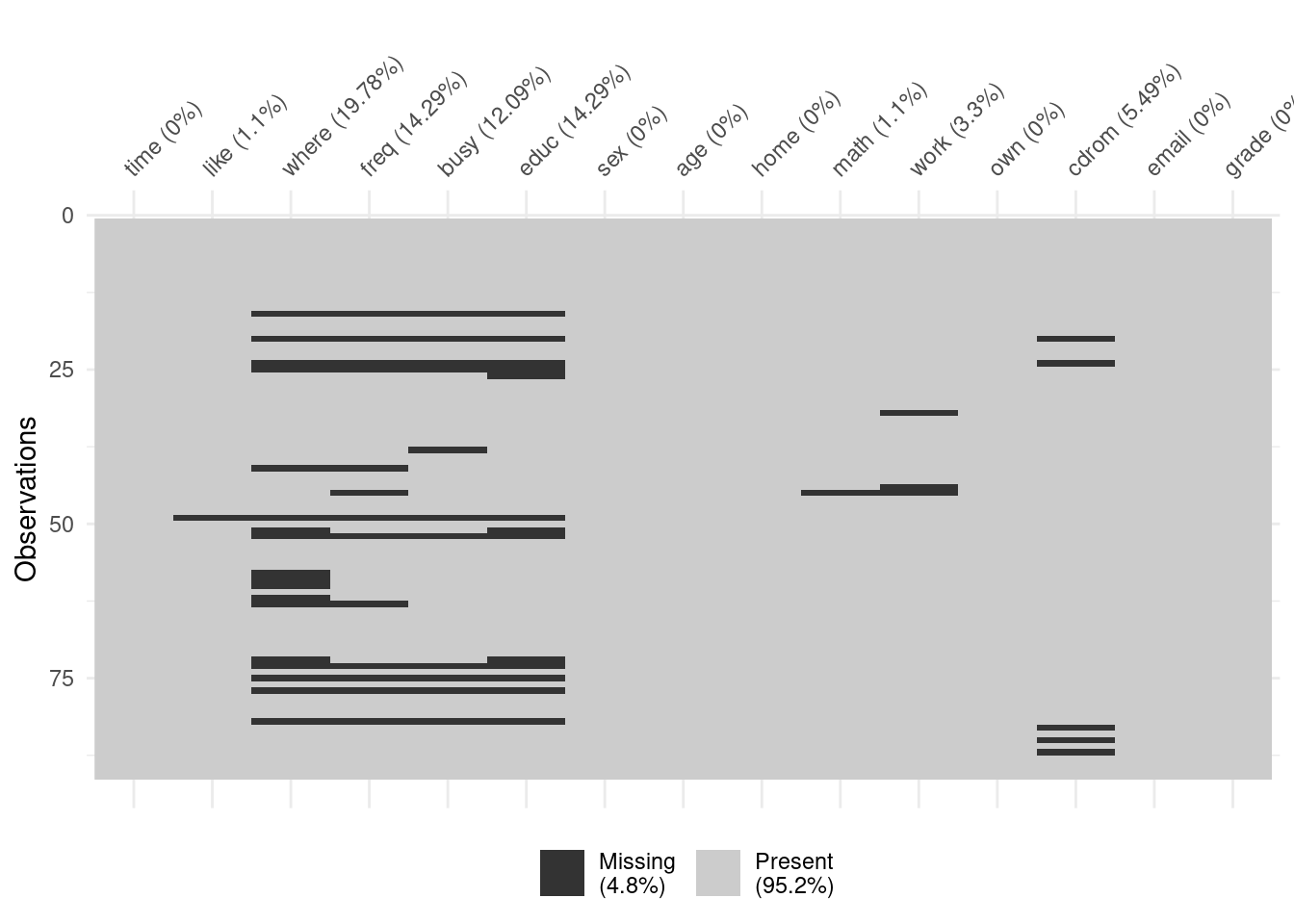
novo_vide_game <- remove_missing(videogame)
ggplot(novo_vide_game, aes(age, freq))+
geom_point()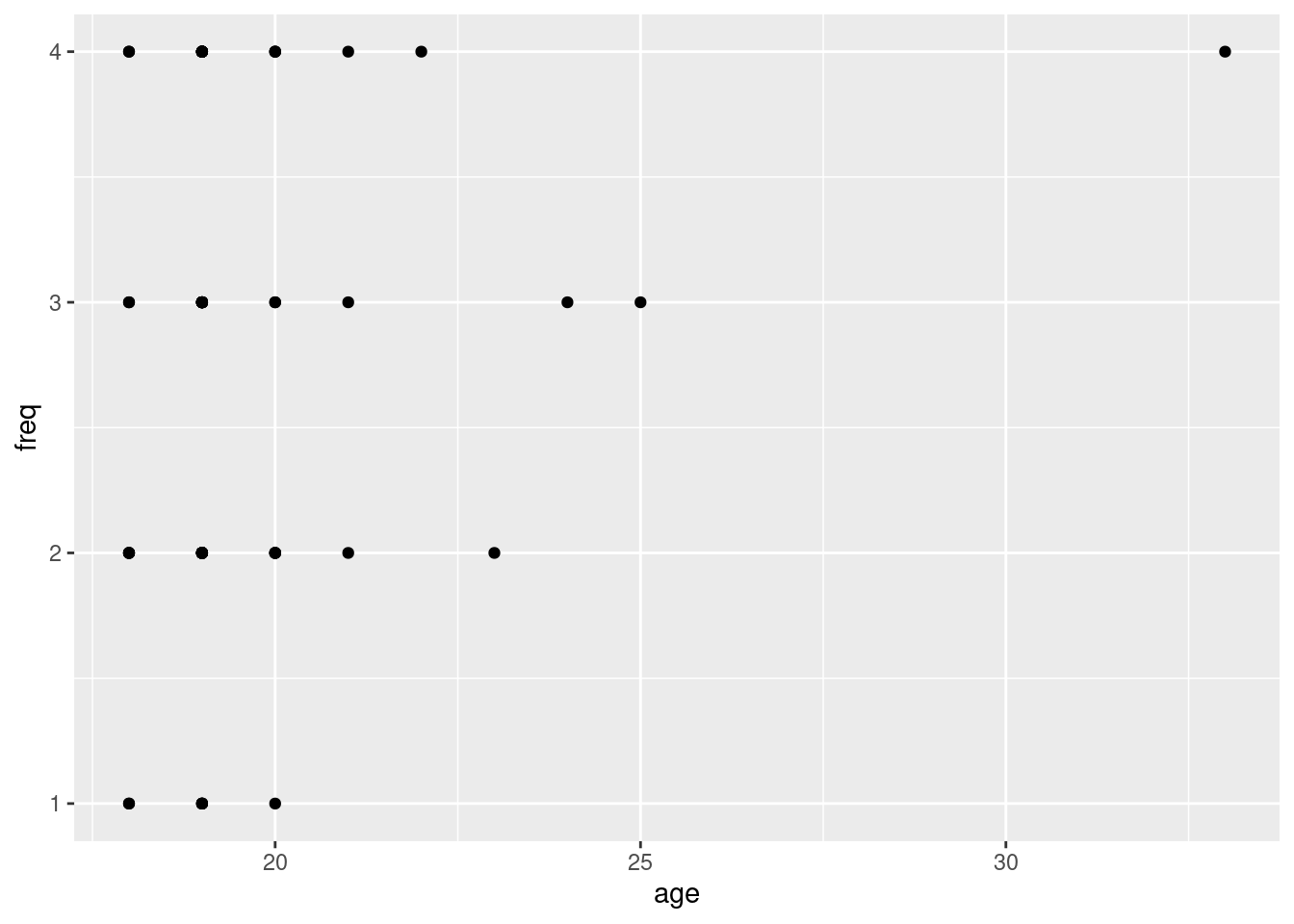
novo_vide_game$freq<-factor(novo_vide_game$freq, levels = c( "4", "3", "2", "1"), ordered = TRUE)
novo_vide_game$grade<-factor(novo_vide_game$grade, levels = c( "0", "1", "2", "3", "4"), ordered = TRUE)
#---Modelagem
modelo <- clm(freq~age, data=novo_vide_game)
predprob <- data.frame(age = novo_vide_game$age)
fv <- predict(modelo, newdata = predprob, type = "prob")$fit
modelo2 <- clm(grade~time, data=novo_vide_game)
predprob2 <- data.frame(time = novo_vide_game$time)
fv2 <- predict(modelo2, newdata = predprob2, type = "prob")$fit
#---Diagnose
logitgof(novo_vide_game$freq, fv, g=4, ord = TRUE)
#>
#> Hosmer and Lemeshow test (ordinal model)
#>
#> data: novo_vide_game$freq, fv
#> X-squared = 8.8602, df = 8, p-value = 0.3542
lipsitz.test(modelo, g=4)
#>
#> Lipsitz goodness of fit test for ordinal response
#> models
#>
#> data: formula: freq ~ age
#> LR statistic = 2.7104, df = 3, p-value = 0.4385
scale_test(modelo)
#> Tests of scale effects
#>
#> formula: freq ~ age
#> Df logLik AIC LRT Pr(>Chi)
#> <none> -83.993 175.99
#> age 1 -82.552 175.10 2.8807 0.08965 .
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
nominal_test(modelo)
#> Tests of nominal effects
#>
#> formula: freq ~ age
#> Df logLik AIC LRT Pr(>Chi)
#> <none> -83.993 175.99
#> age
logitgof(novo_vide_game$grade, fv2, g=5, ord = TRUE)
#>
#> Hosmer and Lemeshow test (ordinal model)
#>
#> data: novo_vide_game$grade, fv2
#> X-squared = 14.973, df = 7, p-value = 0.03634
lipsitz.test(modelo2, g=5)
#>
#> Lipsitz goodness of fit test for ordinal response
#> models
#>
#> data: formula: grade ~ time
#> LR statistic = 5.4831, df = 4, p-value = 0.2412
scale_test(modelo2)
#> Tests of scale effects
#>
#> formula: grade ~ time
#> Df logLik AIC LRT Pr(>Chi)
#> <none> -56.238 118.48
#> time 1 -55.365 118.73 1.7456 0.1864
nominal_test(modelo2)
#> Tests of nominal effects
#>
#> formula: grade ~ time
#> Df logLik AIC LRT Pr(>Chi)
#> <none> -56.238 118.48
#> time 1 -54.625 117.25 3.2263 0.07247 .
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#---Inferencia
summary(modelo)
#> formula: freq ~ age
#> data: novo_vide_game
#>
#> link threshold nobs logLik AIC niter max.grad cond.H
#> logit flexible 65 -83.99 175.99 5(0) 7.87e-10 1.4e+05
#>
#> Coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> age -0.1923 0.1253 -1.535 0.125
#>
#> Threshold coefficients:
#> Estimate Std. Error z value
#> 4|3 -4.759 2.482 -1.917
#> 3|2 -3.611 2.457 -1.469
#> 2|1 -1.613 2.452 -0.658
summary(modelo2)
#> formula: grade ~ time
#> data: novo_vide_game
#>
#> link threshold nobs logLik AIC niter max.grad cond.H
#> logit flexible 65 -56.24 118.48 6(0) 4.48e-12 2.5e+01
#>
#> Coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> time 0.04598 0.12085 0.38 0.704
#>
#> Threshold coefficients:
#> Estimate Std. Error z value
#> 2|3 -2.6853 0.5254 -5.111
#> 3|4 0.5143 0.2807 1.8328.2 Uma pesquisadora interessada em entender o efeito de diferentes usos de solo sobre a abundância de morcegos em paisagens agroecológicas desenvolveu uma simulação para gerar dados parecidos com o que irá coletar em breve no campo. Ela utilizou uma abordagem que simula a abundância de uma espécie sob deriva ecológica segundo a Teoria Neutra da Biodiversidade. A simulação gerou os seguintes dados:
set.seed(42)
J <- 5000 # número de indivíduos na comunidade local
theta <- 50 #número fundamental da biodiversidade
m <- 0.05 #taxa de dispersão
comm1a <- coalesc(J, m, theta) #simulação
abund1a <- abund(comm1a) #extração de dados de abundância local
head(abund1a$com) #dados da comunidade local
#> sp ab relab
#> 1 1 161 0.0322
#> 2 2 93 0.0186
#> 3 3 185 0.0370
#> 4 4 86 0.0172
#> 5 5 35 0.0070
#> 6 6 69 0.0138
#histograma da abundância
ggplot(abund1a$com, aes(ab))+
geom_density(aes(col="red", fill="red"))+
theme(legend.position = "non")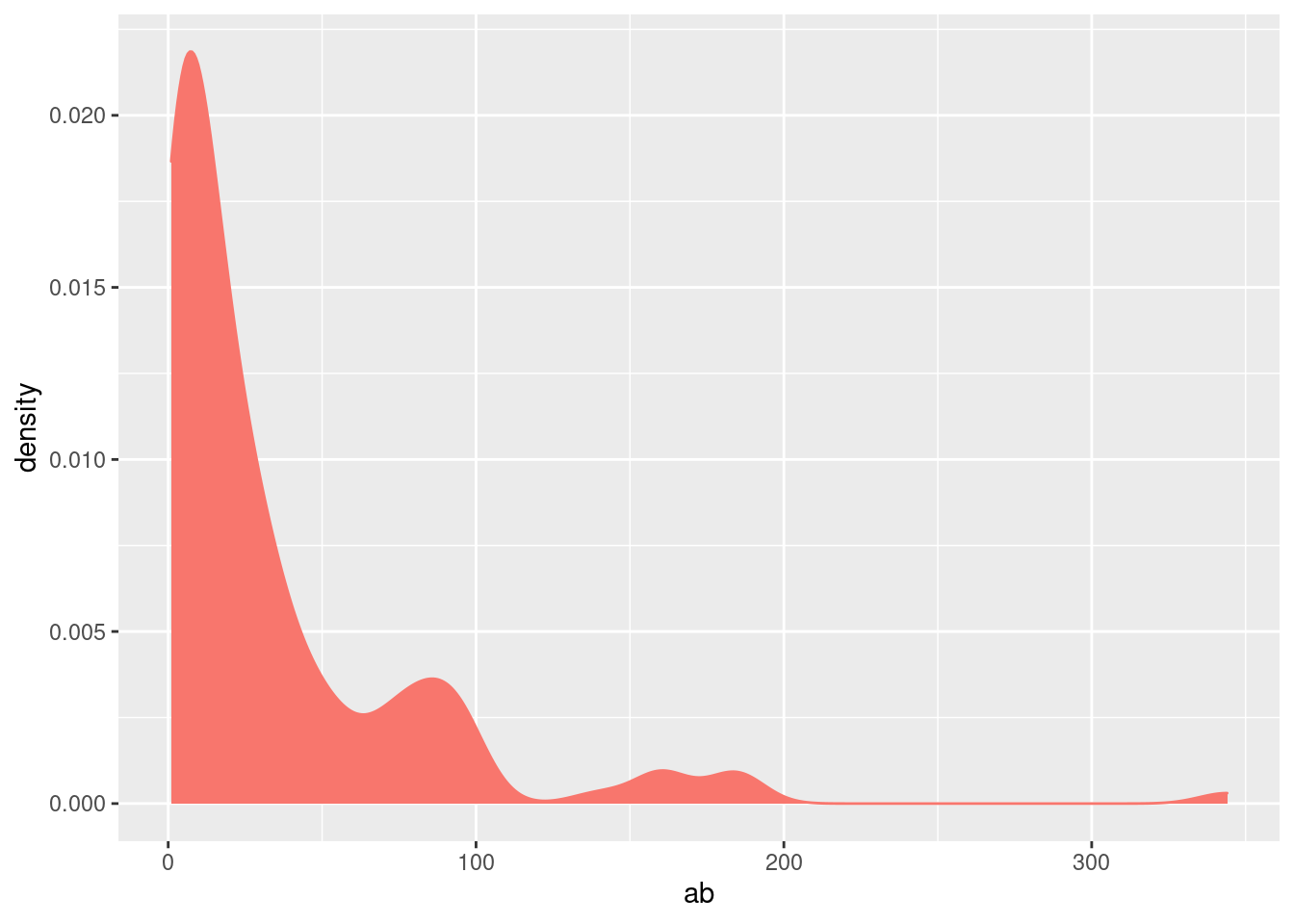
Além disso, a pesquisadora também simulou dados que representam a porcentagem do solo destinado à agricultura:
porc_solo <- rbeta(length(abund1a$com$ab), 10, 90) #simulação uso do solo para agricultura
hist(porc_solo)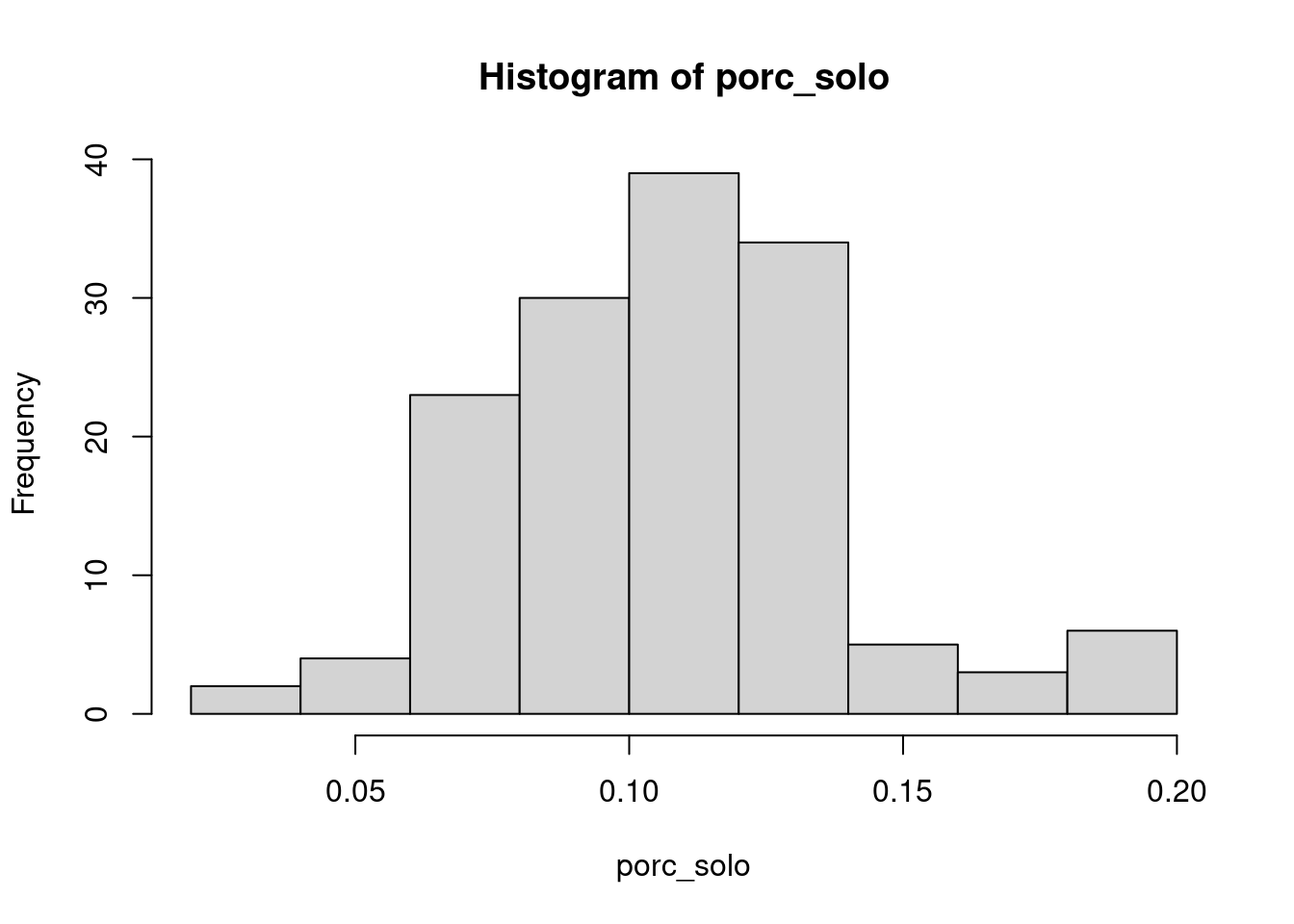
dados_finais <- data.frame(abund=abund1a$com$ab, solo=porc_solo)
head(dados_finais)
#> abund solo
#> 1 161 0.11063484
#> 2 93 0.11498853
#> 3 185 0.05718937
#> 4 86 0.06134667
#> 5 35 0.18910965
#> 6 69 0.12660113
ggplot(dados_finais, aes(solo, abund))+
geom_point()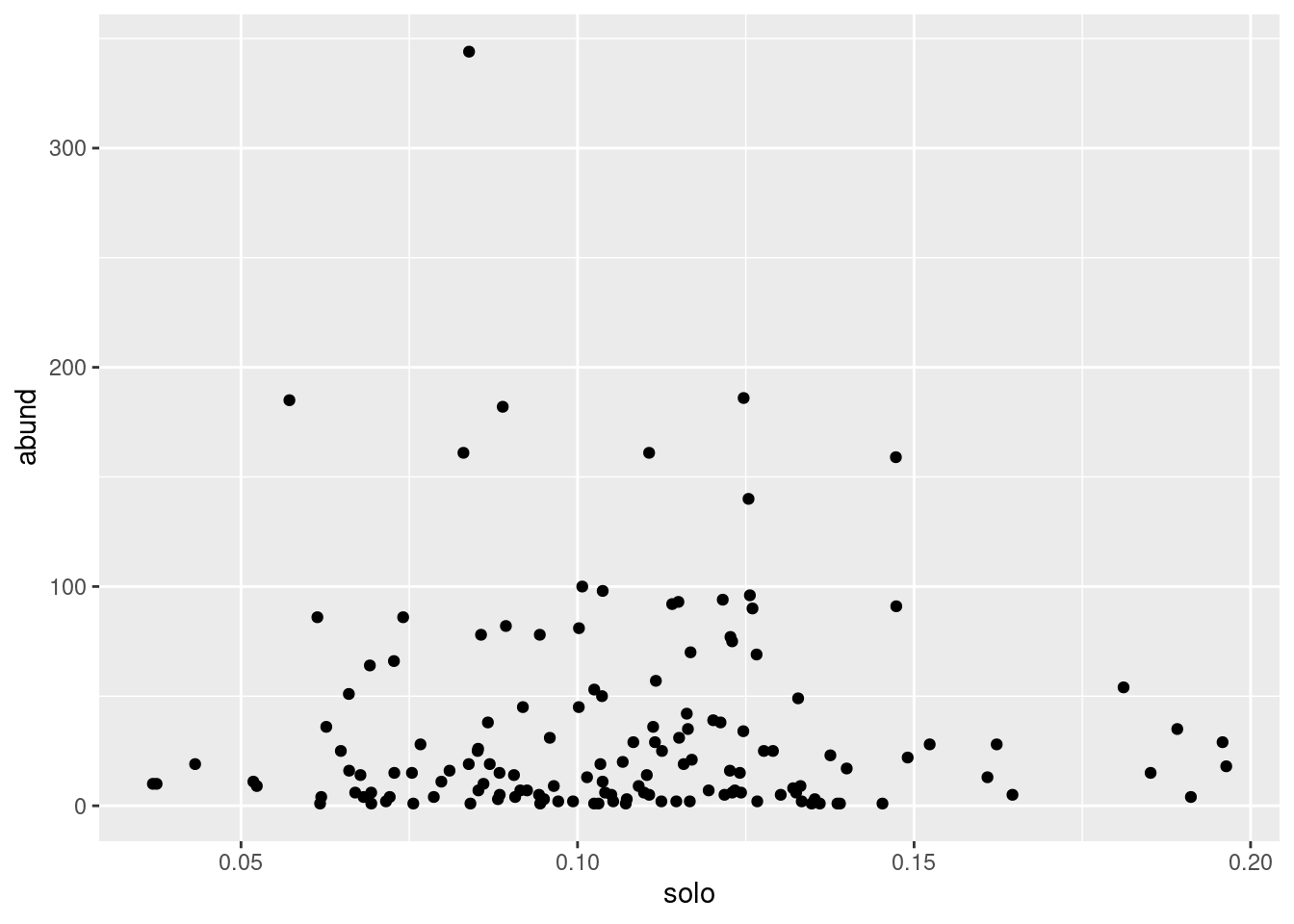
Agora com esses dados ela pode ter uma idéia do que esperar quando for pra campo. Ajude a pesquisadora a construir um modelo linear generalizado que seja adequado para modelar a abundância desta espécie de morcego em função da porcentagem de agricultura. Lembre-se de que ela vai precisar diagnosticar o modelo antes de utilizá-lo para fazer uma inferência. Por fim, interprete os resultados e sugira uma possível interpretação para a pesquisadora.
Solução:
#--- Poisson GLM
Ord_plot(dados_finais$abund)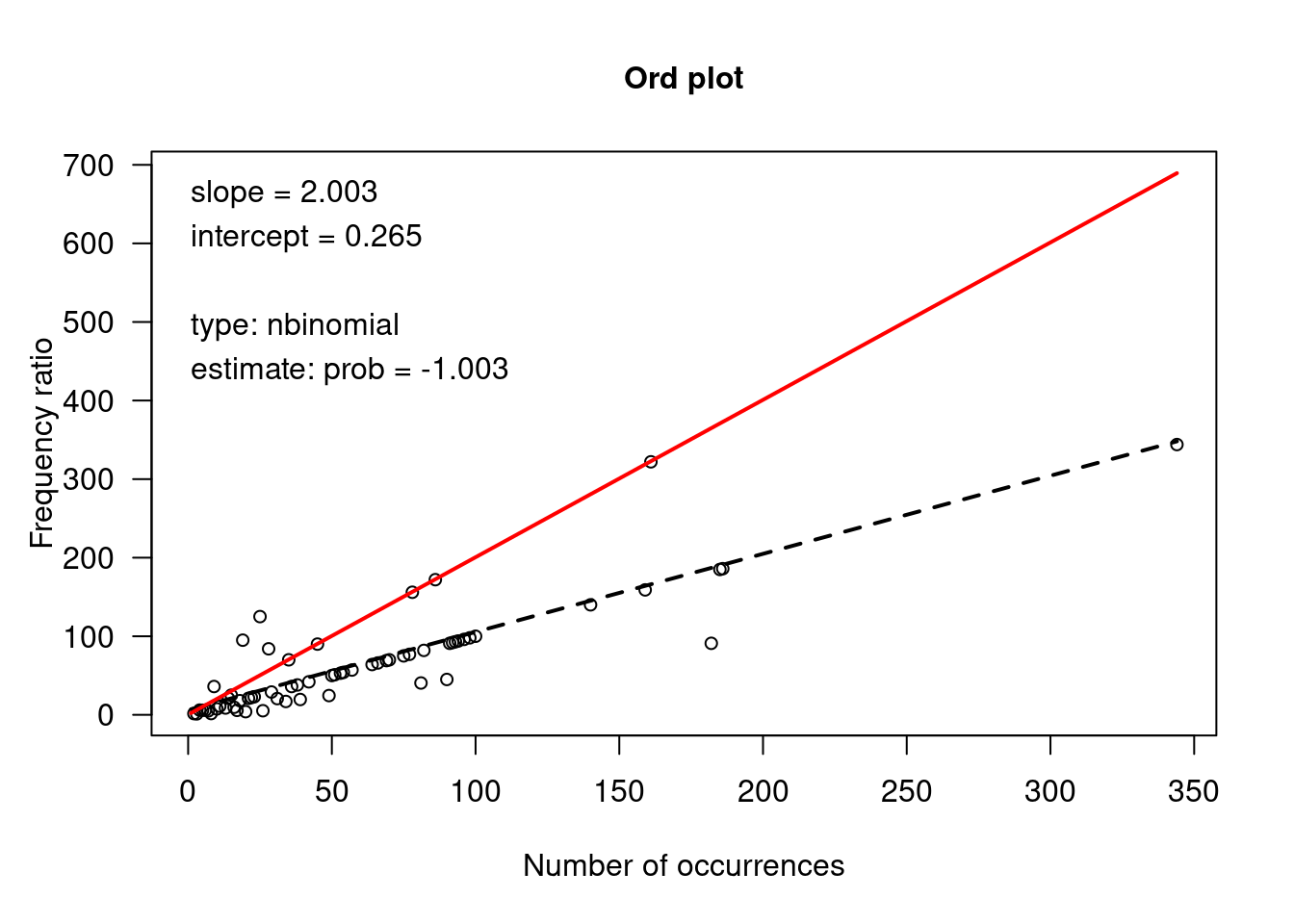
##--- Modelagen
mod <- glm(abund ~ solo, family = poisson, data=dados_finais)
##--- Diagnose
simulateResiduals(fittedModel = mod, plot = TRUE)#vários problemas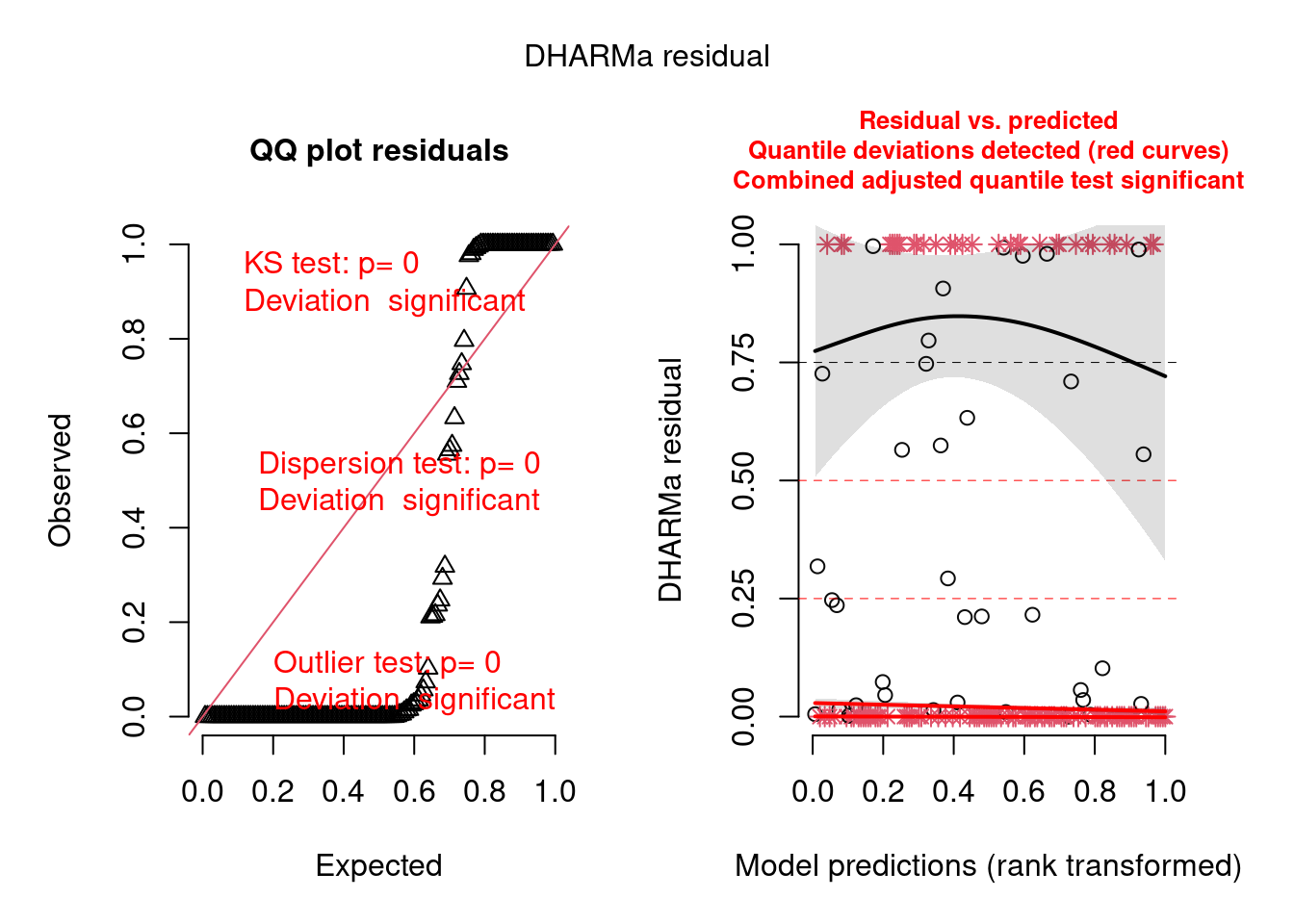
#> Object of Class DHARMa with simulated residuals based on 250 simulations with refit = FALSE . See ?DHARMa::simulateResiduals for help.
#>
#> Scaled residual values: 1 1 1 1 0.7261688 1 1 1 1 1 1 1 0.9929127 1 1 1 0.7470071 0 0 0 ...
#--- Negative Binomial GLM
mod2 <- glm.nb(abund ~ solo, data=dados_finais)
##--- Modelagem
simulateResiduals(fittedModel = mod2, plot = TRUE)#resíduos OK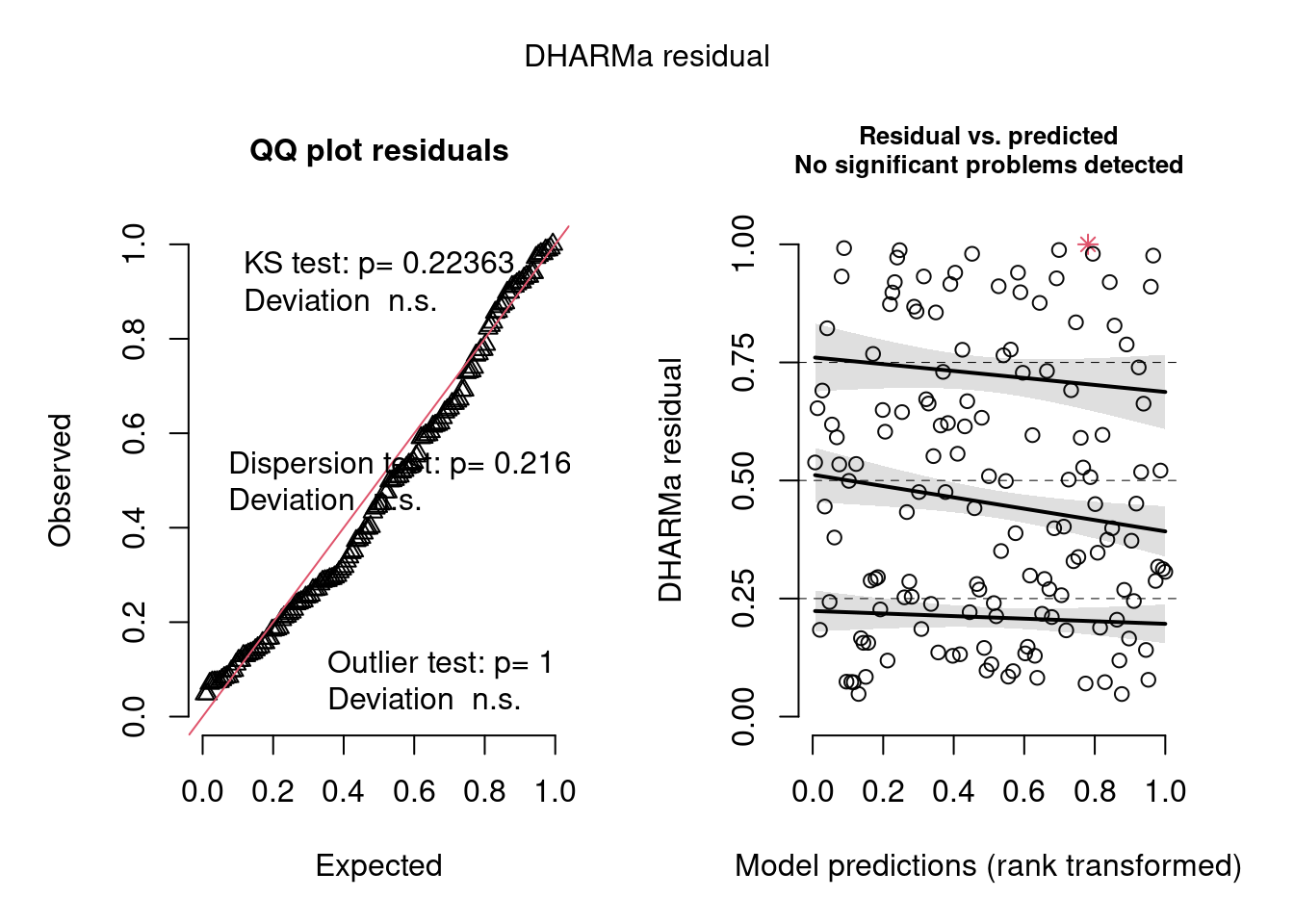
#> Object of Class DHARMa with simulated residuals based on 250 simulations with refit = FALSE . See ?DHARMa::simulateResiduals for help.
#>
#> Scaled residual values: 0.98 0.916 0.9761553 0.9102875 0.6904015 0.8732464 0.8223153 0.92 0.987653 1 0.876 0.828 0.7650707 0.94 0.8980019 0.972 0.672 0.3506113 0.2914758 0.2701042 ...
##--- Inferencia
parameters(mod2)
#> Parameter | Log-Mean | SE | 95% CI | z | p
#> --------------------------------------------------------------
#> (Intercept) | 3.66 | 0.36 | [ 2.92, 4.42] | 10.26 | < .001
#> solo | -1.20 | 3.21 | [-7.86, 5.66] | -0.37 | 0.709
standardize_parameters(mod2)#tamanho do efeito
#> # Standardization method: refit
#>
#> Parameter | Coefficient (std.) | 95% CI
#> ------------------------------------------------
#> (Intercept) | 3.53 | [ 3.34, 3.74]
#> solo | -0.04 | [-0.25, 0.18]
#>
#> (Response is unstandardized)
rsquared(mod2)
#> Response family link method
#> 1 abund Negative Binomial(0.6941) log nagelkerke
#> R.squared
#> 1 0.0008249756
ggplot(dados_finais, aes(solo, abund))+
geom_point()+
geom_smooth(method = "glm.nb")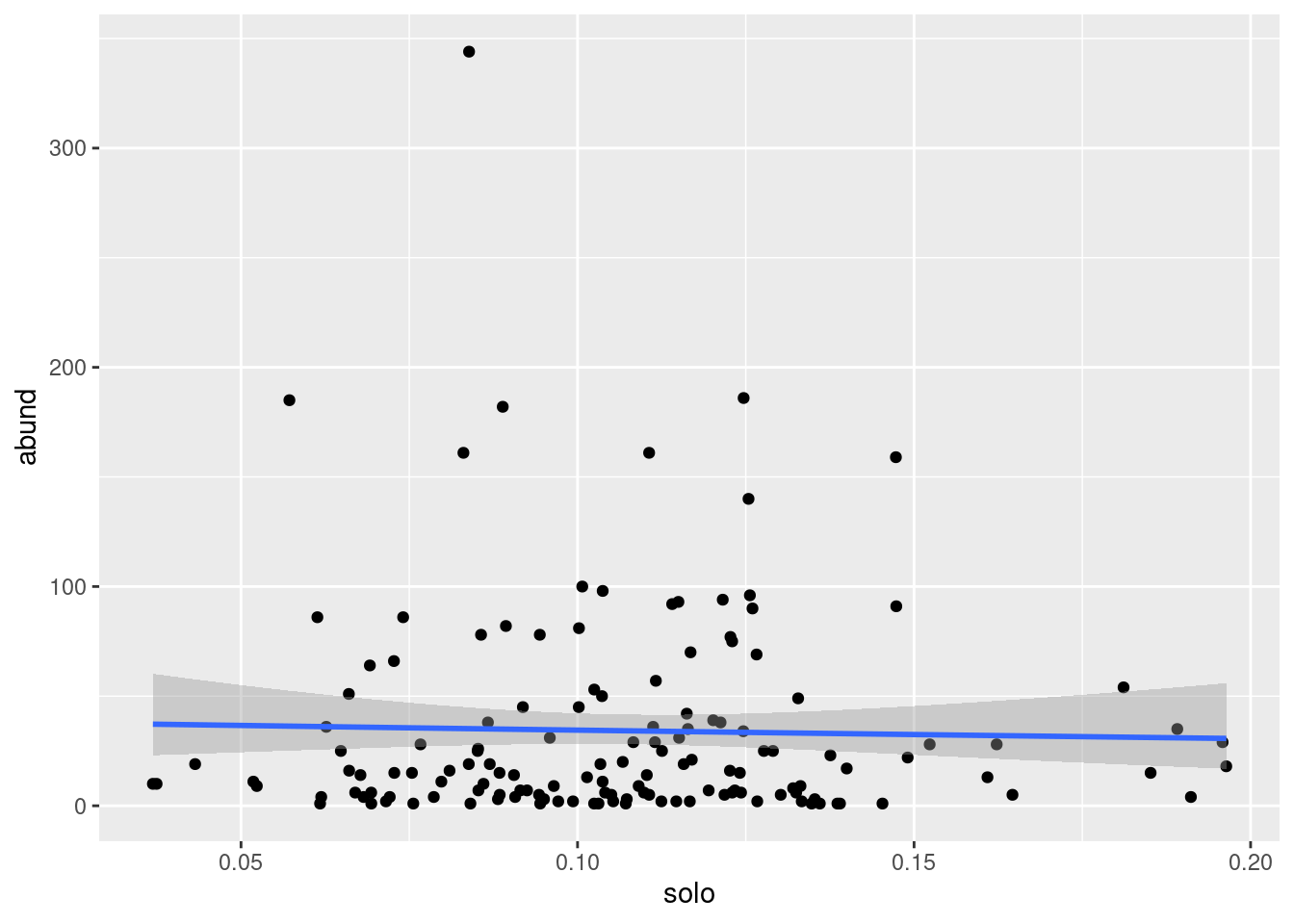
Resposta: existe um ligeiro efeito negativo da porcentagem de agricultura sobre a abundância desta espécie de morcego. Agora a pesquisadora está mais tranquila porque já sabe como serão os dados e possíveis resultados que terá.